Double integral is mainly used to find the surface area of a 2d figure, and it is denoted using ‘ ∫∫’. We can easily find the area of a rectangular region by double integration. If we know simple integration, then it will be easy to solve double integration problems. So, first of all, we will discuss some basic rules of integration.

Integration is a significant part of the calculus, and there are many types of integrations like simple integration, double integration, and triple integration. We usually use integral calculus to find the area and volume on a very large scale, by which simple formulas or computations could determine.

Double Integral Definition

In mathematics, double integral is defined as the integrals of a function in two variables over a region in R², i.e. the real number plane. The double integral of a function of two variables, say f(x, y) over a rectangular region can be denoted as:

\(\iint_{R}f(x,y)\ dA =\iint_{R}f(x,y)\ dx\ dy\)

Double Integration Rule

In calculus, we usually follow the rules and formulas to perform any integration method. To solve integration problems, you must have studied various ways such as integration by parts, integration by substitution, or formulas. In the case of double integration also, we will discuss here the rule for double integration by parts, which is given by;

Properties of Double Integral

The properties of double integrals are as follows:

• ∫_x=a^b ∫_y=c^d f(x,y)dy.dx = ∫_y=c^d∫_x=a^b f(x,y)dx.dy
• ∫∫(f(x,y) ± g(x,y)) dA = ∫∫f(x,y)dA ± ∫∫g(x,y)dA
• If f(x,y) < g(x,y), then ∫∫f(x,y)dA < ∫∫g(x,y)dA
• k ∫∫f(x,y).dA = ∫∫k.f(x,y).dA
• ∫∫_R∪Sf(x,y).dA = ∫∫_Rf(x,y).dA+∫∫_sf(x,y).dA

Also, read:

Double Integral Area

Let z = f(x, y) be defined over a domain D in the xy plane, and we need to find the double integral of z. If we divide the required region into vertical stripes and carefully find the endpoints for x and y, i.e. the limits of the region, then we can use the Double integral Formula;

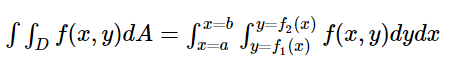
And, if we divide the required region into horizontal stripes and carefully find the endpoints for x and y, i.e. the limits of the region, then we can use the formula:

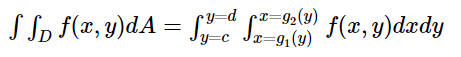
If the function z is a continuous function, then;

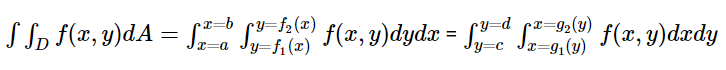
Double Integral in Polar Coordinates

The double integral \(\iint_{R}f(x,y)\ dA\) n rectangular coordinates can be converted to a double integral in polar coordinates as:

\(\iint_{R}f(x,y)\ dA=\iint_{R}f(r\ cos\theta, r\ sin\theta)\ r\ dr\ d\theta\)

This can also be written as:

\(\iint_{R}f(x,y)\ dA=\int_{\theta_1}^{\theta_2}\int_{r_1}^{r_2}f(r\ cos\theta, r\ sin\theta)\ r\ dr\ d\theta\)

Where, 

f(r cosθ, r sinθ) = f(r, θ)

In this type of double integral, first, we have to integrate f(r,θ) with respect to r between the limits r = r₁ and r = r₂ treating θ as a constant and the resulting expression is integrated with respect to θ from θ₁ to θ₂. Here r₁ and r₂ may be constants or functions of θ.

In this case, first, we have to integrate f(r,θ) with respect to θ between the limits θ = θ₁ and θ = θ₂ and treating r as a constant and the resulting expression are integrated with respect to r and that time the function of θ will be constant.

Double Integral Examples

Question 1:- Evaluate the double integral (x²+y²)dx dy Or ∬(x²+y²)dx dy

Solution: Let us say, I = ∬(x²+y²)dx dy

I = ∫[∫(x²+y²)dx]dy

I = ∫[x³/3+y²x]dy

I = x³y/3+xy³/3

I = [xy(x²+y²)]/3 + C

Question 2:- Solve the function ∫∫x.logx.dx.dy

Solution: Assume I = ∫∫x.logx.dx.dy

First, let us take the inner integral on the functions ∫x.logx dx.

By integration by parts rule, we can solve the above integral;

∫x.logx dx = ∫(logx)x dx

The logarithmic function on the x function with another function x is not integrated directly. So, we can take it as;

u = log x and dv = x dx

So, du = (1/x) dx.v = x²/2

Therefore, ∫x.logx.dx = (logx)x²/2 − ∫(x²/2)(1/x)dx

= x²/2(logx)−1/2 ∫x.dx

Hence, ∫x.logx.dx = x²/2(logx) − 1/4x²

This is the result obtained under the integration by parts for the inner integral. Now, operate it with the outer integral functions by:

∫∫x.logx.dxdy = ∫[x²/2(logx) − 1/4x²]dy

I = ∫[x²/2(logx)]dy − ∫[1/4x²]dy

I = (x²y/2) (log x) – 1/4x²y.dy + C

Question 3: Find the double integral (x+y)dx dy, i.e. ∬(x+y)dx dy

Solution: Let us say, I = ∬(x+y) dx dy

I = ∫[∫(x+y)dx]dy

I = ∫[x²/2+yx]dy

I = x²y/2+xy²/2

I = (xy/2)(x+y) + C

Question 4: Evaluate: \(\int_{1}^{2}\int_{4}^{6}\frac{x}{y^2}dx\ dy\)

Solution:

Given,

Let us perform the integration with respect to y.

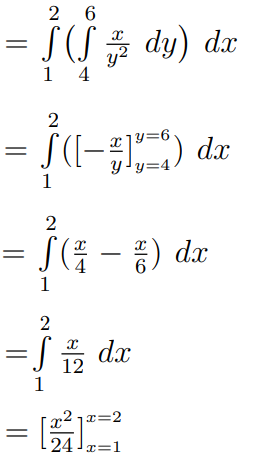
= (2)²/24 – (1)²/24

= (4 – 1)/24

= 3/24

= 1/8

Practice Problems

Practice more questions based on this concept. Here are a few double integral problems which you can work on to understand the concept in a better way.

1. Evaluate: ∫∫x² y³ dx dy
2. Estimate: ∫∫x e^x dx dy
3. Calculate the double integral of 1/xy.
4. Find the double integral xy dx dy, ∫∫xy dx dy.