Equation of A Plane
The equation of a plane in the three-dimensional space is defined with the normal vector and the known point on the plane. A Vector is a physical quantity that with its magnitude also has a direction attached to it. A normal vector means the line which is perpendicular to the plane. With reference to an origin, the position vector basically denotes the location or position (in a 3D Cartesian system) of a point. The Cartesian equation of a plane in 3 Dimensional space and vectors are explained in this article.
Equation of a Plane in Three Dimensional Space
Generally, the plane can be specified using four different methods. They are:
- Two intersecting lines
- A line and point (not on a line)
- Three non-collinear points (Three points are not on the line)
- Two parallel and the non-coincident line
- The normal vector and the point
There are infinite planes that lie perpendicular to a specific vector. But only one unique plane exists to a specific point which remains perpendicular to the point while going through it
Let us consider a plane passing through a given point A having position vector \(\vec{a} \) and perpendicular to the vector \(\vec{N} \) . Let us consider a point P(x, y, z) lying on this plane and its position vector is given by \(\vec{r} \) as shown in the figure given below.
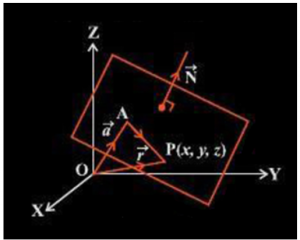
Position vector simply denotes the position or location of a point in the three-dimensional Cartesian system with respect to a reference origin.
For point P to lie on the given plane it must satisfy the following condition:
\(\vec{AP} \) is perpendicular to \(\vec{N} \) , i.e. \(\vec{AP} \).\(\vec{N} \) =0
From the figure given above it can be seen that,
\(\vec{AP} \) = ( \(\vec{r} \) – \(\vec{a} \))
Substituting this value in \(\vec{AP} \) . \(\vec{N} \) =0, we have (\(\vec{r} \) – \(\vec{a} \)). \(\vec{N} \) =0
This equation represents the vector equation of a plane.
We will assume that P, Q and R points are regarded as x1, y1, z1 and x2, y2, z2 in respectively to change the equation into the Cartesian system. A, B and C will be the assumed direction ratios. Thus,
\(\vec{r} = x\hat{i}+y\hat{j}+z\hat{k}\)\(\vec{a} = x_{1}\hat{i}+y_{1}\hat{j}+z_{1}\hat{k}\)
\(\vec{N} = A\hat{i}+B\hat{j}+C\hat{k}\)
Substituting these values in the vector equation of a plane, we have
\((\vec{r}-\vec{a}). \vec{N} = 0\)\((( x\hat{i}+y\hat{j}+z\hat{k})- (x_{1}\hat{i}+y_{1}\hat{j}+z_{1}\hat{k})). A\hat{i}+B\hat{j}+C\hat{k} = 0\)
\([(x-x_{1})\hat{i}+ (y-y_{1})\hat{j}+ (z-z_{1})\hat{k}](A\hat{i}+B\hat{j}+C\hat{k})= 0\)
\(A(x-x_{1})+ B(y-y_{1})+ C(z-z_{1})= 0\)
This gives us the Cartesian equation of a plane. To learn more about the equation of a plane in three dimensions and three-dimensional geometry download BYJU’S – The Learning App.