Latus Rectum
In Mathematics, a conic section is defined as a curve which is obtained from the intersection of the surface of a cone with a plane. There are three different types of conic sections. They are parabola, ellipse and hyperbola. To define these curves, many important terms are used, such as focus, directrix, latus rectum, locus, asymptote, and so on. In this article, let us discuss the term “Latus Rectum” in detail.
Latus Rectum Definition
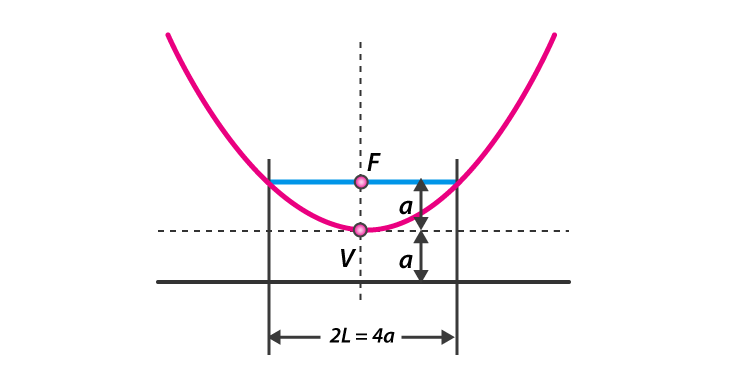
In the conic section, the latus rectum is the chord through the focus, and parallel to the directrix. The word latus rectum is derived from the Latin word “latus” which means “side”, and the “rectum” which means “straight”. Half the latus rectum is called the semi latus rectum. The diagram above shows the latus rectum of a parabola.
Length of Latus Rectum of Parabola
Let the ends of the latus rectum of the parabola, y2=4ax be L and L’. The x-coordinates of L and L’ are equal to ‘a’ as S = (a, 0)
Assume that L = (a, b).
We know that L is a point of the parabola, we have
b2 = 4a (a) = 4a2
Take square root on both sides, we get b = ±2a
Therefore, the ends of the latus rectum of a parabola are L = (a, 2a), and L’ = (a, -2a )
Hence, the length of the latus rectum of a parabola, LL’ is 4a.
Length of Latus Rectum of Hyperbola
Latus rectum of a hyperbola is defined analogously as in the case of parabola and ellipse.
The ends of the latus rectum of a hyperbola are (ae, ±b2/a2), and the length of the latus rectum is 2b2/a.
Latus Rectum of Conic Sections
The summary for the latus rectum of all the conic sections are given below:
| Conic Section | Length of the Latus Rectum | Ends of the Latus Rectum |
| y2 = 4ax | 4a | L = (a, 2a), L’ = (a, -2a) |
| (x2./a2) + (y2./b2) =1 | If a>b; 2b2/a | L = (ae, b2/a), L = (ae, -b2/a) |
| (x2./a2) + (y2./b2) =1 | If b>a; 2a2/b | L = (ae, b2/a), L = (ae, -b2/a) |
| (x2./a2) – (y2./b2) =1 | 2b2/a | L = (ae, b2/a), L = (ae, -b2/a) |
Latus Rectum Examples
Example 1:
Find the length of the latus rectum whose parabola equation is given as, y2 = 12x.
Solution:
y2 = 12x
⇒ y2 = 4(3)x
Since y2 = 4ax is the equation of parabola, we get value of a:
a = 3
Hence, the length of the latus rectum of a parabola is = 4a = 4(3) =12.
Example 2:
Find the length of the latus rectum of an ellipse 4x2 + 9y2 – 24x + 36y – 72 = 0.
Solution:
Given: 4x2 + 9y2 – 24x + 36y – 72 = 0
⇒ ( 4x2 – 24x ) + ( 9y2 + 36y ) – 72 = 0
⇒ 4( x2 -6x ) + 9( y2 + 4y ) – 72 = 0
⇒ 4[ x2 – 6x +9 ] + 9[ y2 + 4y +4 ] = 144
⇒ 4( x – 3 )2 + 9( y + 2 )2 = 144
⇒ {( x – 3 )2/ 36} + {( y + 2 )2/ 16 } = 1
⇒ {( x – 3 )2/ 62} + {( y + 2 )2/ 42 } = 1
⇒ a = 3 and b = 2
Therefore, the length of the latus rectum of an ellipse is given as:
= 2b2/a
= 2(2)2 /3
= 2(4)/3
= 8/3
Hence, the length of the latus rectum of ellipse is 8/3.
For more Maths-related articles and solved problems, register with BYJU’S – The Learning App and download the app to learn with ease.