Cos Meaning
The cos meaning, in Mathematics, relates to the cosine function, which we learn in the most important concept of geometry, i.e., trigonometry. The cosine function is one of the three major functions of trigonometry. These three functions are also termed as trigonometric ratios, which are sine, cosine and tangent.
The cos meaning in trigonometry defines the cosine of an angle. This angle is an acute angle in a right angled triangle, which is considered to find the ratios. Thus, cosine of an angle, in a right-triangle, is equal to the ratio of adjacent side of that angle and hypotenuse of the triangle.
Cos Function
As we have already discussed in the introduction, cos is the cosine function of a right triangle in trigonometry. Cos function is the ratio of adjacent side and hypotenuse. It helps us to find the length of the sides of the triangle, irrespective of given angle.
Suppose we have a right triangle and α is the angle between adjacent side and hypotenuse, then as per the cos function, we can write
Cos α = Adjacent Side/Hypotenuse
Cos Formula
From the above given expression, we get the cosine function equal to the ratio of adjacent sides of the respective angle and hypotenuse.
Let us take a right-angled triangle ABC, which is right-angled at C, as per given below:
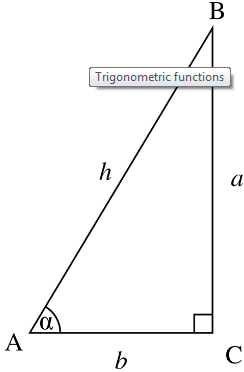
Now, as per the cos meaning, in triangle ABC,
Cos α = Adjacent Side/Hypotenuse
Cos α = AC/AB
Cos α = b/h
which is the required formula.
Cos Table
The value of cos is derived for different values of angles such as 0°, 30°, 45°, 60°, 90°, etc. These values are required to find the sides of the triangle. To solve the problems based on trigonometry, it is required to learn these values, given in the below table:
|
Cos Degrees |
Values |
|
Cos 0° |
1 |
|
Cos 30° |
√3/2 |
|
Cos 45° |
1/√2 |
|
Cos 60° |
1/2 |
|
Cos 90° |
0 |
|
Cos 120° |
-1/2 |
|
Cos 150° |
-√3/2 |
|
Cos 180° |
-1 |
|
Cos 270° |
0 |
|
Cos 360° |
1 |
Cos Identities
In trigonometry, identities are used to solve many trigonometric equations. Here are cos identities which are mostly used:
- cos2 (α) + sin2 (α) = 1
- cos α = 1/sec α
- cos (−α) = cos (α)
- arccos (cos (α)) = α + 2kα [where k=integer]
- Cos (2α) = cos2 (α) − sin2 (α)
- cos (α) = sin (π/2 − α)
Cos Law
The cos law or cosine law defines the relationship between the sides and the angles of the triangle. This law is also known as the law of cosine or cosine rule. According to this law,
c2 = a2 + b2 − 2ab cos α
Where a, b and c are the sides of the triangle.