In Calculus, a line integral is an integral in which the function to be integrated is evaluated along a curve. A line integral is also called the path integral or a curve integral or a curvilinear integral. In this article, we are going to discuss the definition of the line integral, formulas, examples, and the application of line integrals in real life.

Line Integral Definition

A line integral is integral in which the function to be integrated is determined along a curve in the coordinate system. The function which is to be integrated may be either a scalar field or a vector field. We can integrate a scalar-valued function or vector-valued function along a curve. The value of the line integral can be evaluated by adding all the values of points on the vector field.

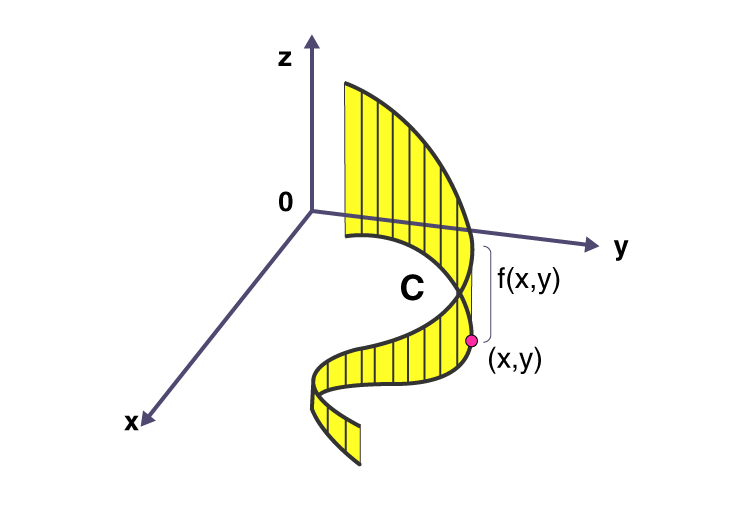
Line Integral Formula

The line integral for the scalar field and vector field formulas are given below:

Line integral Formula for Scalar Field

For a scalar field with function f: U ⊆ Rⁿ → R, a line integral along with a smooth curve, C ⊂ U is defined as:

∫_C f(r) ds = \(\int_{a}^{b}\) f[r(t)] |r’(t)| dt

Here, r: [a, b]→C is an arbitrary bijective parametrization of the curve.

r (a) and r(b) gives the endpoints of C and a < b.

Line integral Formula for Vector Field

For a vector field with function, F: U ⊆ Rⁿ → Rⁿ, a line integral along with a smooth curve C ⊂ U, in the direction “r” is defined as:

∫_C F(r). dr = \(\int_{a}^{b}\) F[r(t)] . r’(t)dt.

Here, “.” represents the dot product.

Application of Line Integral

Line integral has several applications. A line integral is used to calculate the surface area in the three-dimensional planes. Some of the applications of line integrals in the vector calculus are as follows:

• A line integral is used to calculate the mass of wire.
• It helps to calculate the moment of inertia and centre of mass of wire.
• It is used in Ampere’s Law to compute the magnetic field around a conductor.
• In Faraday’s Law of Magnetic Induction, a line integral helps to determine the voltage generated in a loop.
• Line integral helps to calculate the work done by a force on a moving object in a vector field.

Line Integral Example

Go through the line integral example given below:

Example: Evaluate the line integral ∫_C F. dr where F(x, y, z) = [P(x, y, z), Q(x, y, z), R(x, y, z)] = (z, x, y), and C is defined by the parametric equations, x = t², y = t³ and z = t² , 0 ≤ t ≤ 1.

Solution:

Given that, the function, F(x, y, z) = [P(x, y, z), Q(x, y, z), R(x, y, z)] = (z, x, y)

Parametric equations: x = t², y = t³ and z = t² , 0 ≤ t ≤ 1.

We know that,

∫_C F. dr = ∫_C P dx + Q dy + R dz

∫_C F. dr = \(\int_{0}^{1}\) z(t) x’(t)dt + x(t) y’(t)dt + y(t) z’(t)dt

= \(\int_{0}^{1}\) t² (2t)dt + t² (3t²)dt + t³ (2t) dt

= \(\int_{0}^{1}\) 2t³ dt + 3t⁴ dt + 2t⁴dt

= \(\int_{0}^{1}\) (5t⁴ + 2t³) dt

= \(\left ( 5\frac{t^{5}}{5}+2\frac{t^{4}}{4} \right )_{0}^{1}\)

Substitute the limits, we get,

∫_C F. dr = 3/2

Therefore, the line integral for the given function is 3/2.

Keep visiting BYJU’S – The Learning app for more Maths related articles and download the app to get the interactive videos.