Linear pair of angles are formed when two lines intersect each other at a single point. The angles are said to be linear if they are adjacent to each other after the intersection of the two lines. The sum of angles of a linear pair is always equal to 180°. Such angles are also known as supplementary angles. The adjacent angles are the angles which have a common vertex. Hence, here as well the linear angles have a common vertex. Also, there will be a common arm which represents both the angles. A real-life example of a linear pair is a ladder which is placed against a wall, forms linear angles at the ground.

Linearity represents one which is straight. So here also, linear angles are the one which is formed into a straight line. The pair of adjacent angles here are constructed on a line segment, but not all adjacent angles are linear. Hence, we can also say, that linear pair of angles is the adjacent angles whose non-common arms are basically opposite rays.

Explanation for Linear Pair of Angles

When the angle between the two lines is 180°, they form a straight angle. A straight angle is just another way to represent a straight line. A straight line can be visualized as a circle with an infinite radius. A line segment is any portion of a line which has two endpoints. Also, a portion of any line with only one endpoint is called a ray. A line segment with A and B as two endpoints is represented as \(\overline{AB}\). The figure shown below represents a line segment AB and the two arrows at the end indicate a line.

If a point O is taken anywhere on the line segment AB as shown, then the angle between the two line segments AO and OB is a straight angle i.e. 180°.

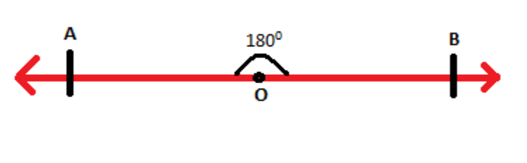
Consider a ray \(\overrightarrow{OP}\) stand on the line segment \(\overline{AB}\) as shown:

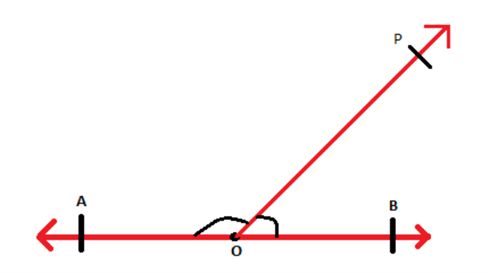
The angles which are formed at O are ∠POB and ∠POA. It is known that the angle between the two line segments AO and OB is 180°. therefore, the angles ∠POB and ∠POA add up to 180°.

Thus, ∠POB + ∠POA = ∠AOB = 180°

∠POB and ∠POA are adjacent to each other and when the sum of adjacent angles is 180° then such angles form linear pair of angles.

The above discussion can be stated as an axiom.

Also, read:

Axioms

Axiom 1: If a ray stands on a line then the adjacent angles form a linear pair of angles.

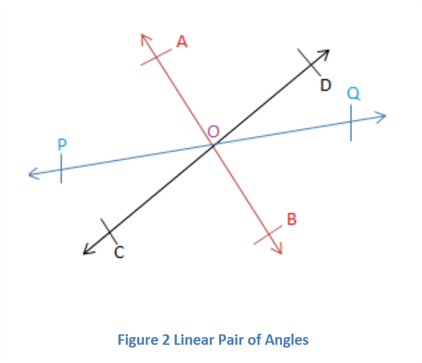
In the figure above, all the line segments pass through the point O as shown. As the ray OA lies on the line segment CD, angles ∠AOD and ∠AOC form a linear pair. Similarly, ∠QOD and ∠POD form a linear pair and so on.

The converse of the stated axiom is also true, which can also be stated as the following axiom.

Axiom 2: If two angles form a linear pair, then uncommon arms of both the angles form a straight line.

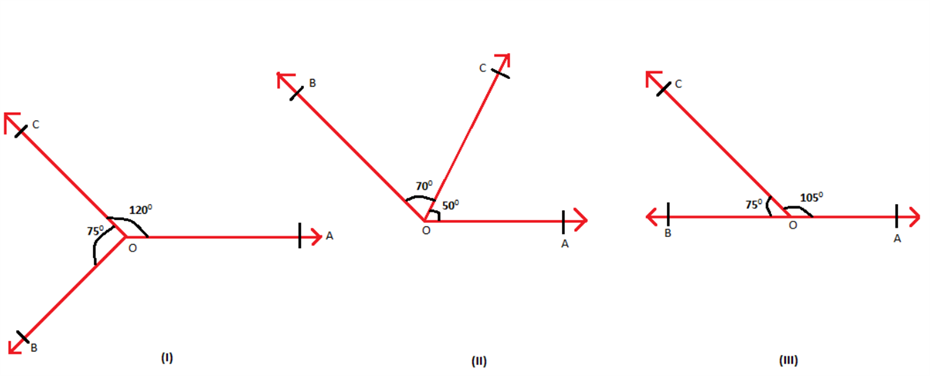
Figure 3 Adjacent angles with different measures

In the figure shown above, only the last one represents a linear pair, as the sum of the adjacent angles is 180°. Therefore, AB represents a line. The other two pairs of angles are adjacent but they do not form a linear pair. They do not form a straight line.

The two axioms mentioned above form the Linear Pair Axioms and are very helpful in solving various mathematical problems.

Example

Suppose two angles ∠AOC and ∠ BOC form a linear pair at point O in a line segment AB. If the difference between the two angles is 60°. Then find both the angles.

Solution: Given, ∠AOC and ∠ BOC form a linear pair

So, ∠AOC + ∠ BOC =180° ………(1)

Also given,

∠AOC – ∠ BOC = 60° ………(2)

Adding eq. 1 and 2, we get;

2∠AOC = 180° + 60° = 240°

∠AOC = 240°/2 = 120°

Now putting the value of ∠AOC in equation 1, we get;

∠BOC = 180° – ∠AOC = 180° – 120°

∠BOC = 60°

There is a lot more to learn about lines and angles. To know more about properties of pair of angles, download BYJU’S – The Learning App from Google Play Store.