What is the Magnitude of a Vector?

As we know, the vector is an object which has both the magnitude as well as direction. To find the magnitude of a vector, we need to calculate the length of the vector. Quantities such as velocity, displacement, force, momentum, etc. are vector quantities. But speed, mass, distance, volume, temperature, etc. are scalar quantities. The scalar has the only magnitude, whereas the vectors have both magnitude and direction.

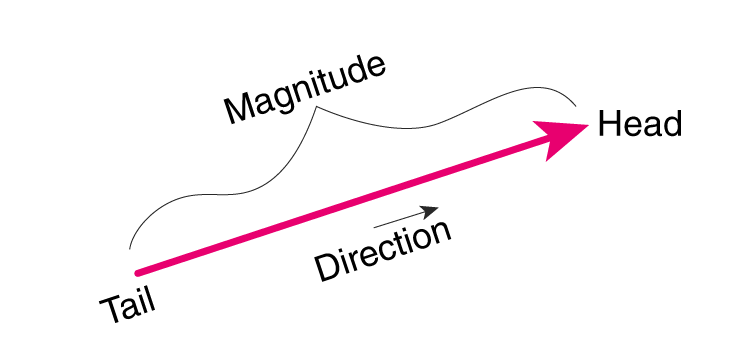
The magnitude of a vector formula is used to calculate the length for a given vector (say v) and is denoted as |v|. So basically, this quantity is the length between the initial point and endpoint of the vector. To calculate the magnitude of the vector, we use the distance formula, which we will discuss here.

Magnitude of a Vector Formula

Suppose, AB is a vector quantity that has magnitude and direction both. To calculate the magnitude of the vector \(\vec{AB}\), we have to calculate the distance between the initial point A and endpoint B. In XY – plane, let A has coordinates (x₀, y₀) and B has coordinates (x₁, y₁). Therefore, by distance formula, the magnitude of vector \(\vec{AB}\), can be written as;

|\({\vec{AB}}\)| = \(\sqrt{(x_1 – x_0)^2 + (y_1 – y_0)^2}\)

Now if the starting point is at (x, y) and the endpoint is at the origin, then the magnitude of a vector formula becomes;

|\(\vec{AB}\)| = \(\sqrt{x^2 + y^2}\)

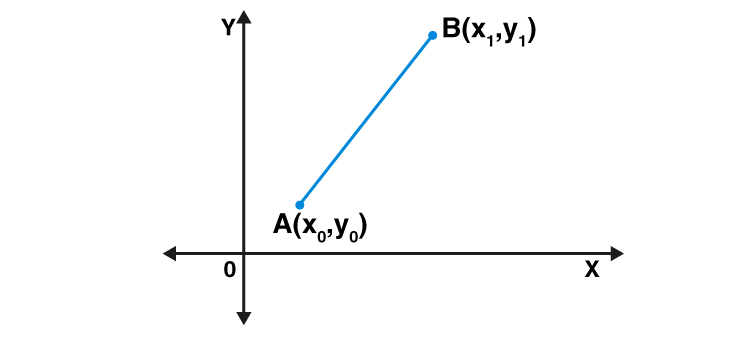
Direction of a vector

The direction of a vector is nothing but the measurement of the angle which is made with the horizontal line. One of the methods to find the direction of the vector \(\vec{AB}\) is;

tan α = y/x; endpoint at 0.

Where x is the change in horizontal line and y is the change in a vertical line.

Or tan α = \(\frac{y_1 – y_0}{x_1 – x_0}\) ; where (x_{0 ,} y₀) is initial point and (x₁ , y₁) is the endpoint.

Problems on Magnitude of a Vector

Problem 1: Find the magnitude of the vector \(\vec{AB}\) whose initial point, A is (1, 2) and endpoint, B is (4, 3).

Solution: Given, A is (1, 2) and B is (4, 3) as the initial point and endpoint respectively.

Therefore, x₀ = 1 & y₀ = 2 and x₁ = 4 & y₁ = 3

Using distance formula,

|\(\vec{AB}\)| = \(\sqrt{(x_1 – x_0)^2 + (y_1 – y_0)^2}\)

|\(\vec{AB}\)| = \(\sqrt{(4 – 1)^2 + (3 – 2)^2}\)

|\(\vec{AB}\)| = \(\sqrt{3^2 + 1^2}\)

|\(\vec{AB}\)| = \(\sqrt{9 + 1}\)

|\(\vec{AB}\)| = \(\sqrt{10}\)

|\(\vec{AB}\)| ≈ 3.2

The magnitude of \(\vec{AB}\) ≈ 3.2

If we have to calculate the magnitude of a 3d vector, then there would be three coordinates points and we can represent the magnitude of the vector \(\vec{v}\) as;

\(\vec{v}\) = xi + yj + zk

|\(\vec{v}\)| = \(\sqrt{x^2+y^2+z^2}\)

Let us consider a 3d object.

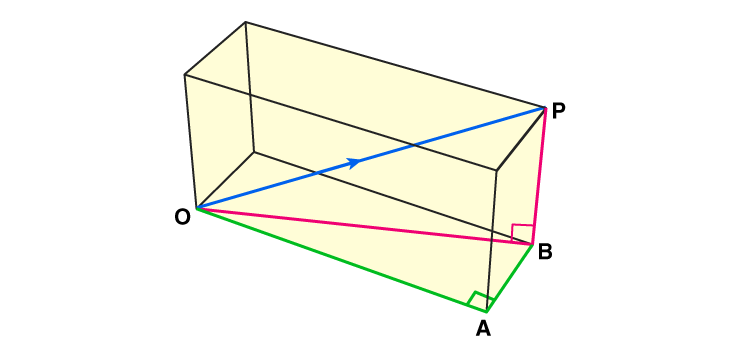
In the figure, you can see the magnitude of the vector is represented by the vector \(\vec{V}\) (blue line), which is the length of the arrow representing \(\vec{V}\). So, the length of the OP is the magnitude of \(\vec{V}\). To calculate the magnitude, we have to use Pythagoras theorem here, for the triangles, OBP and OAB.

In triangle OBP (1)

OP² = OB² + BP²

And in triangle OAB (2)

OB² = OA² + AB²

From equation 1 and 2 we get,

OP² = OA²+ AB² + BP²

\(\vec{OP}=\sqrt{OA^2 +AB^2 + BP^2}\)

Therefore, the magnitude of a 3d vector xi + yj + zk = \(\sqrt{x^2 +y^2 + z^2}\)

Problem 2 Find the magnitude of a 3d vector 2i + 3j + 4k.

Solution: We know, the magnitude of a 3d vector xi + yj + zk = \(\sqrt{x^2 +y^2 + z^2}\)

Therefore, the magnitude of a 3d vector 2i + 3j + 4k = \(\sqrt{2^2 +3^2 + 4^2}\)

= \(\sqrt{4 + 9 + 16}\)

= \(\sqrt{29}\)

Hence, the magnitude of a 3d vector 2i + 3j + 4k ≈ 5.38

Download BYJU’S – The Learning App and enjoy learning with us by getting interactive and fun videos.