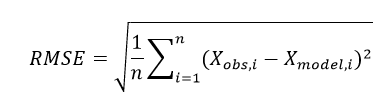In statistics, the concept of mean squared error is an essential measure utilized to determine the performance of an estimator. It is abbreviated as MSE and is necessary for relaying the concepts of precision, bias and accuracy during the statistical estimation. Learn the formula for MSE along with root mean square error formula in this article.

Statistics is all about organization and analysis of numerical data which is usually related to some statistical research or survey. Statistics can be defined as a mathematical analysis which uses quantified models and representations as well as reports about a given set of data or observations from some real-world situation.

The process of gathering and observing data and then summarizing and analyzing it via numerical formulas and calculations is known as statistical analysis. In this method, the analyst first requires a population from which a sample or a set of samples is chosen to start with the research. If our data set belongs to a sample of a bigger population, then the analyst can extend presumptions over the population-based on statistical results.

Definition

The measure of mean squared error needs a target of prediction or estimation along with a predictor or estimator, which is said to be the function of the given data. MSE is the average of squares of the “errors”.

Here, the error is the difference between the attribute which is to be estimated and the estimator. The mean square error may be called a risk function which agrees to the expected value of the loss of squared error. This difference or the loss could be developed due to the randomness or due to the estimator is not representing the information which could provide a more accurate estimate.

The mean squared error can also be referred to the second moment of the error, measured about the origin. It includes both the variance and bias of the estimator. If an estimator is an unbiased estimator, then its MSE is the same as the variance of the estimator. The unit of MSE is the same as the unit of measurement for the quantity which is being estimated.

Mean Squared Error Formula

Let us suppose that X_i is the vector denoting values of n number of predictions. Also, X_i is a vector representing n number of true values. Then, the formula for mean squared error is given below:

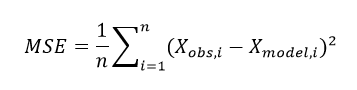
In more general language, if θ be some unknown parameter and θ_{obs, i} be the corresponding estimator, then the formula for mean square error of the given estimator is:

It is to be noted that technically MSE is not a random variable, because it is an expectation. It is subjected to the estimation error for a certain given estimator of θ with respect to the unknown true value. Therefore, the estimation of the mean squared error of an estimated parameter is actually a random variable.

Root Mean Square Error Formula

The root mean square error (RMSE) is a very frequently used measure of the differences between value predicted value by an estimator or a model and the actual observed values. RMSE is defined as the square root of differences between predicted values and observed values. The individual differences in this calculation are known as “residuals”. The RMSE estimates the magnitude of the errors. It is a measure of accuracy which is used to perform comparison forecasting errors from different estimators for a specific variable, but not among the variables, since this measure is scale-dependent.