A fraction represents a part of whole. For example, it tells how many slices of a pizza left or eaten with respect to the whole pizza, like, one-half, three-quarters.

Parts of a Fraction:

Every fraction is made up of two terms, namely

Numerator, which is the top part of a fraction.

Denominator, which is the bottom part of a fraction.

Example: \(\frac{5}{9}\),

Here, 5 is the Numerator and 9 is the Denominator.

Types of Fraction:

Fractions can be of two types Proper Fractions and Improper Fractions.

If both the numerator and denominators are positive and numerator less than denominator such fractions are called proper fraction.

Ex: \(\frac{3}{8},\frac{9}{11}\) etc.

Whereas fractions having numerator greater than the denominator is called improper fraction.

Ex: \(\frac{8}{7},\frac{5}{2}\) etc.

Improper fractions can also be written using the combination of a whole number and a fraction term known as Mixed Fraction.

Ex: \(\frac{29}{8} = 3\frac{5}{8}\) , \(\frac{7}{3} = 2\frac{1}{3}\)

 

In this article we learn about multiplication of fractions and various other operations related to fractions. 

Multiplication of Fractions:

Multiplication involving a fraction is as simple as multiplication of any other real number. In order to multiply the fractions we need to follow the step given:

Multiply all the numerator terms and all the denominator terms that would result in numerator and denominator of the fraction respectively.

\(Product \;\; of \;\; Fraction = \frac{Product \;\; of \;\; Numerator}{Product \;\; of \;\; Denominator}\)

Eg: \(\frac{3}{5} \times \frac{1}{4} \times \frac{7}{9} = \frac{3 \times 1 \times 7}{5 \times 4 \times 9} = \frac{7}{60}\)

 

This is true for a proper fraction and an improper fraction. To find the product of any numbers involving a mixed fraction, convert the mixed fraction into an improper fraction and multiply.

As we already know that the multiplication is the repeated addition of numbers, therefore adding the number of times a fraction would result in their multiplication.

Eg: \(5 \times \frac{1}{6} = \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6}\) = \(= \frac{5}{6}\)

FRACTION AS AN OPERATOR

When a fraction is referred as an operator it means it is a part of whole of something. The word ‘of’ denotes the multiplication. For example, 2/4 of 2 pizzas means 1 pizza i.e. 2/4 × 2=1.

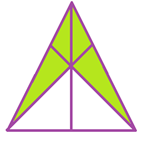
Another example say, the shaded portions in the figure given below represent 4/6 of the triangle.

Example 1: Evaluate \(\frac{2}{3} \times \frac{5}{9}\)

Solution:  Product of rational numbers= (Product of numerators)/(Product of denominators)

(2/3) x (5/9) = (2×5)/(3×9) = 10/27

Example 2: Evaluate \(3\frac{1}{4} \times 3\)

Solution:  To find the product convert the mixed fraction into an improper fraction and then multiply.

\(3\frac{1}{4} = \frac{(3 \times 4) + 1}{4}\)

\(= \frac{13}{4}\)

Now multiplying the terms, we have:

\(\frac{13}{4} \times 3 = \frac{13 \times 3}{4} = \frac{39}{4}\)

Example 3: Find 5/6 of 12

Solution: 5/6 of 12 means,

\(\frac{5}{6} \times 12 = \frac{5 \times 12}{6} = 10\)

To solve more problems on the topic, download BYJU’S – The Learning App and watch interactive videos. Also, take free tests to practice for exams.