Number Lines
In Maths, number lines are the horizontal straight lines in which the integers are placed in equal intervals. All the numbers in a sequence can be represented in a number line. This line extends indefinitely at both ends.
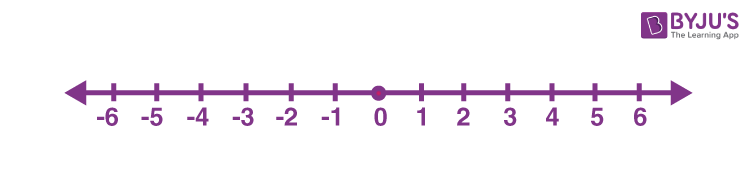
In the above figure, we can see a number line where integers are placed. Here, the positive and negative integers are placed on either side of the zero.
What is a Number Line?
A number line is a pictorial representation of numbers on a straight line. It’s a reference for comparing and ordering numbers. It can be used to represent any real number that includes every whole number and natural number. Just to recollect, the whole number is a set of numbers that include all counting numbers (1, 2, 3,4,5,6 …….) and zero (0), whereas the natural number is the set of all counting numbers i.e. 1, 2, 3, 4, 5, 6……..
Writing numbers on a number line make it easier to compare the numbers. From the above figure, we can see that the integers on the left side are smaller than the integers on the right side. For example, 0 is less than 1, -1 is less than 0, -2 is less than -1, and so on.
Numbers on a Number Line
Arithmetic operations of numbers can be better explained on a number line. To begin with, one must know to locate numbers on a number line. Zero is the middle point of a number line. All (natural numbers) positive numbers occupy the right side of the zero whereas negative numbers occupy the left side of zero on the number line. As we move on to the left side value of a number decreases. For example, 1 is greater than -2. In a number line, integers, fractions, and decimals can also be represented easily. Check out the links given below to learn more.
| Representation of Numbers in a Number line | |
|---|---|
| Representation Of Fraction On The Number Line | Rational numbers on a number line |
| Representation Of Decimals On Number Line | Represent Linear Inequalities In One Variable On Number Line |
Important Notes:
- On a number line, a number on the left is always less than a number on the right.
- Similarly, a number on the right is always greater than a number on the left.
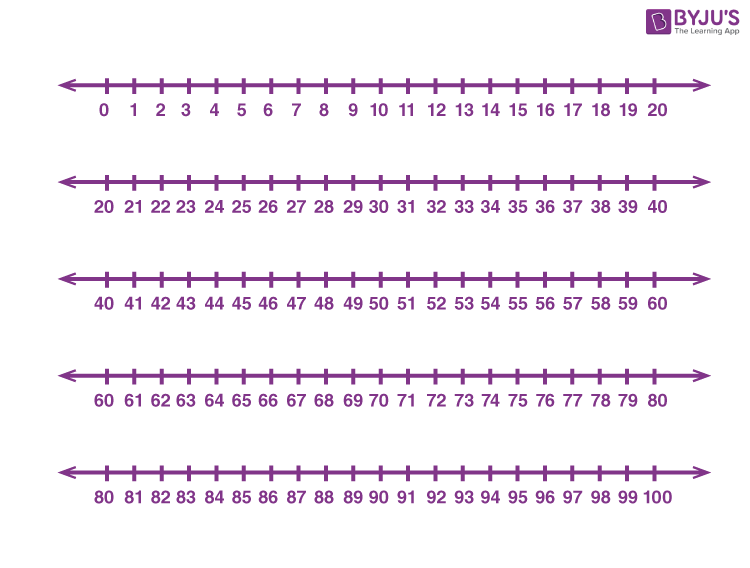
Number Line 1 to 100
Here are the number lines from 1 to 100 numbers. As we already we can extend the number line indefinitely, thus students can also try to draw the line beyond 100, to practice.
Addition on Number Lines
Adding Positive Numbers
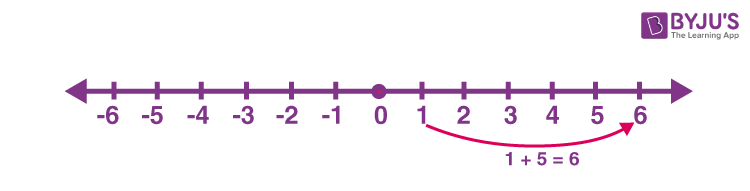
When we add two positive numbers, the result will always be a positive number. Hence, on adding positive numbers direction of movement will always be to the right side.
For example, addition of 1 and 5 (1 + 5 = 6)
Here the first number is 1 and the second number is 5; both are positive. First, locate 1 on the number line. Then move 5 places to the right will give 6.
Adding Negative Numbers
When we add two negative numbers, the result will always be a negative number. Hence, adding negative numbers direction of movement will always be to the left side.
For example, the addition of -2 and -3
Here, the first number is -2 and the second number is -3; both are negative. Locate -2 on the number line. Then move 3 places to the left will give -5.
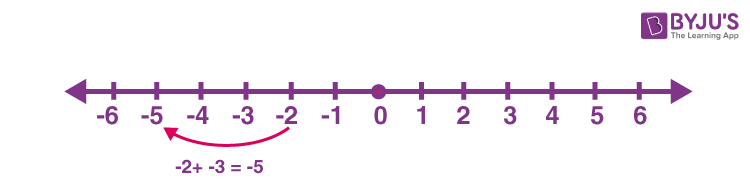
Subtraction on Number Line
Subtracting Positive Numbers
When we subtract two positive numbers, move to the left as far as the value of the second number.
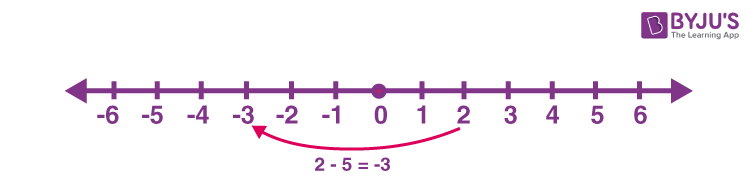
For example, subtract 5 from 2
Here the first number is 2 and the second number is 5; both are positive. First, locate 2 on the number line. Then move 5 places to the left will give -3.
Subtracting Negative Numbers
When we subtract two negative numbers, move to the right as far as the value of the second number.
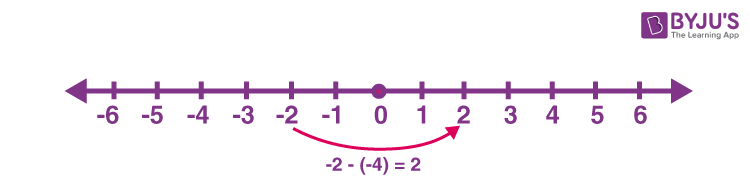
For example, subtract -4 from -2
First, locate -2 on the number line. Then move 4 places to the right will give 2.
Learn More: Operations of Integers on Number Line
Practice Questions
- Add 3 and -9 on the number line.
- Subtract 8 from -2 on the number line.
- Draw a number line representing whole numbers.
- Show the negative integers using a number line
To solve more problems and to watch interactive videos on the topic, keep visiting BYJU’S and download BYJU’S – The Learning App.