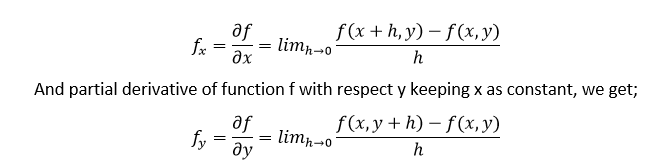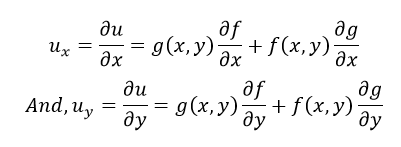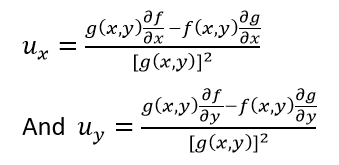The partial derivative is used in vector calculus and differential geometry. In Mathematics, sometimes the function depends on two or more variables. Here, the derivative converts into the partial derivative since the function depends on several variables. In this article, We will learn about the definition of partial derivatives, their formulas, partial derivative rules such as chain rule, product rule, quotient rule with more solved examples.

Table of contents:

• Definition
• Symbol
• Formula
• Partial differentiation
• Rules
  • Product Rule
  • Quotient Rule
  • Power Rule
  • Chain Rule
• Partial Derivative of Natural Log
• Examples

Partial Derivative Definition

Suppose, we have a function f(x, y), which depends on two variables x and y, where x and y are independent of each other. Then we say that the function f partially depends on x and y. Now, if we calculate the derivative of f, then that derivative is known as the partial derivative of f. If we differentiate the function f with respect to x, then take y as a constant and if we differentiate f with respect to y, then take x as a constant.

Partial Derivative Symbol

In mathematics, the partial derivative of any function having several variables is its derivative with respect to one of those variables where the others are held constant. The partial derivative of a function f with respect to the differently x is variously denoted by f’_x,f_x, ∂_xf or ∂f/∂x. Here ∂ is the symbol of the partial derivative.

Example: Suppose f is a function in x and y then it will be expressed by f(x, y). So, the partial derivative of f with respect to x will be ∂f/∂x keeping y as constant. It should be noted that it is ∂x, not dx. ∂f/∂x is also known as f_x.

Partial Derivative Formula

If f(x,y) is a function, where f partially depends on x and y and if we differentiate f with respect to x and y then the derivatives are called the partial derivative of f. The formula for partial derivative of f with respect to x taking y as a constant is given by;

Partial Differentiation

The process of finding the partial derivatives of a given function is called partial differentiation. Partial differentiation is used when we take one of the tangent lines of the graph of the given function and obtaining its slope. Let’s understand this with the help of the below example.

Example: 

Suppose that f is a function of more than one variable such that,

f = x² + 3xy

The graph of z = x² + 3xy is given below:

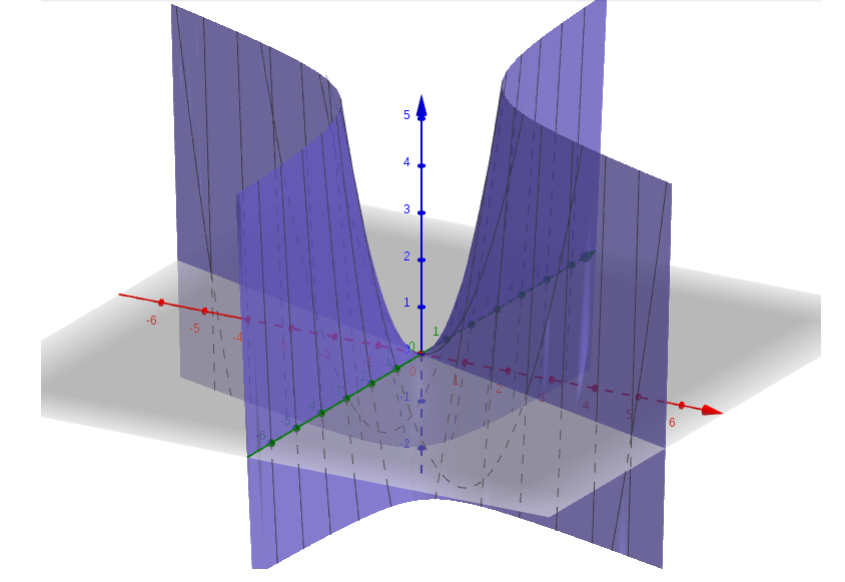
The graph of this function represents a surface in Euclidean space. To each point on this surface, there is an infinite number of tangent lines. Now, we can apply the partial differentiation for choosing one of these lines and finding its slope.
To find the tangent line’s slope to the function at one point, say P(1,1) and parallel to the xz-plane, we treat y as a constant.
By finding the derivative of the equation taking y as a constant, we can get the slope of the given function f at the point (x, y). This can be done as follows.
∂f/∂x = (∂/∂x) (x² + 3xy) = 2x + 3y
The value of ∂f/∂x at (1, 1) is:
2(1) + 3(1) = 5
That means the slope is 5.
Therefore, ∂f/∂x = 5 at (1, 1).

Partial Derivative Rules

Same as ordinary derivatives, partial derivatives follow some rule like product rule, quotient rule, chain rule etc.

Product Rule

If u = f(x,y).g(x,y), then,

Quotient Rule

If u = f(x,y)/g(x,y), where g(x,y) ≠ 0, then;

Power Rule

If u = [f(x,y)]ⁿ then, the partial derivative of u with respect to x and y defined as;

u_x = n|f(x,y)|^n-1∂f/∂x

And u_y = n|f(x,y)|^n-1∂f/∂y

Chain Rule

Here, the chain rule for one independent variable and two independent variables are given below:

Chain Rule for One Independent variable:

Consider that, if x = g(t) and  y=h(t) are the differentiable functions of t, and  z = f(x, y) which is a differentiable function of x and y. Thus z can be written as z = f(g(t), h(t)), is a differentiable function of t, then the partial derivative of the function with respect to the variable “t” is given as:

\(\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x}.\frac{\partial x}{\partial t} +\frac{\partial z}{\partial y}.\frac{\partial y}{\partial t}\)

Here, the ordinary derivatives are determined at “t”, whereas the partial derivatives are evaluated at (x, y)

Chain Rule for Two Independent variables:

Assume that x = g (u, v) and y = h (u, v) are the differentiable functions of the two variables u and v, and also z = f (x, y) is a differentiable function of x and y, then z can be defined as z = f (g (u, v), h (u, v)), which is a differentiable function of u and v. Thus, the partial derivative of the function with respect to the variables are given as:

\(\frac{\partial z}{\partial u} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial u} +\frac{\partial z}{\partial y}\frac{\partial y}{\partial u}\)

and

\(\frac{\partial z}{\partial v} = \frac{\partial z}{\partial x}\frac{\partial x}{\partial v} +\frac{\partial z}{\partial y}\frac{\partial y}{\partial v}\)

Partial Derivative of Natural Logarithm (In)

To find the partial derivative of the natural logarithm “In”, we have to proceed with the same procedure as finding the derivative of the normal function. But, here when we calculate the partial derivative of the function with respect to one independent variable taking another as constant and follow the same thing with others.

Also, see:

Partial Derivative Examples

Example 1: Determine the partial derivative of the function: f (x,y) = 3x + 4y.

Solution:

Given function: f (x,y) = 3x + 4y

To find ∂f/∂x, keep y as constant and differentiate the function:

Therefore, ∂f/∂x = 3

Similarly, to find  ∂f/∂y, keep x as constant and differentiate the function:

Therefore, ∂f/∂y = 4

Example 2: Find the partial derivative of f(x,y) = x²y + sin x + cos y.

Solution:

Now, find out f_x first keeping y as constant

f_x = ∂f/∂x = (2x) y + cos x + 0

= 2xy + cos x

When we keep y as constant cos y becomes a constant so its derivative becomes zero.

Similarly, finding f_y

f_y = ∂f/∂y = x² + 0 + (-sin y)

= x² – sin y

Example 3: Find  ∂f/∂x,  ∂f/∂y,  ∂f/∂z for the given function, f(x, y, z) = x cos z + x²y³e^z

Solution:

To find  ∂f/∂x,  ∂f/∂y,  ∂f/∂z

Given Function:  f(x, y, z) = x cos z + x²y³e^z

∂f/∂x = cos z + 2xy³e^z

∂f/∂y = 3x²y²e^z

∂f/∂z =-x sin z + x²y³e^z

To learn more problems on partial derivatives, and the problems related to differential equations, register with BYJU’S – The Learning App and download the app to learn all the important Maths-related concepts with ease.