CBSE Class 9 Maths Examination 2018: Important 3 marks questions
Important 3 Marks Questions for CBSE Class 9 Maths are provided here. Students should learn the fundamental concepts in Class 9 and it is a crucial stage of student development. It is important for the student to score well in the examination so as to get a good result in the board examination boards, as most of the concepts are repeated in class 10. One prime important subject, of which students are generally afraid of is the Maths subject. Maths requires basics skills and lot of practice to excel in examination. One needs to practice daily few questions in order to score well in the examination. As questions can be framed from any topic, thus it primarily essential to practice marks wise important question.
Here at BYJU’S, we provide important 3 marks questions for CBSE class 9 Maths in order to help students to score good marks in the final examinations. Go through the below-given problems to excel in the exams.
Important 3 Marks Questions for Class 9 Maths for Practice
Practice the important 3 marks questions for CBSE class 9 Maths which are given below. Practising these questions helps the students of class 9 to write the solutions with accuracy and they can be able to manage the time as well during the exams.
Example 1- Simplify \(\left ( \frac{81}{16} \right )^{\frac{-3}{4}}\left [ \left ( \frac{25}{9} \right )^{\frac{-3}{2}} \div \left ( \frac{5}{2} \right )^{-3} \right ]\)
Example 2- Simplify the following by rationalising the denominator
\(\frac{7 \sqrt{3} – 5 \sqrt{2}}{\sqrt{48}+ \sqrt{18}}\)
Example 3- Show that in a right angled triangle the hypotenuse is the longest side.
Example 4- If \(a^{2} + b^{2} + c^{2} = 250\) and \(ab + bc + ca= 3\), then find the value of a+b+c.
Example 5 – If \(x + \frac{1}{x} = 7\), then find the value of \(x^{3} + \frac{1}{x^{3}}\).
Example 6- Find the square root of 3.6 geometrically.
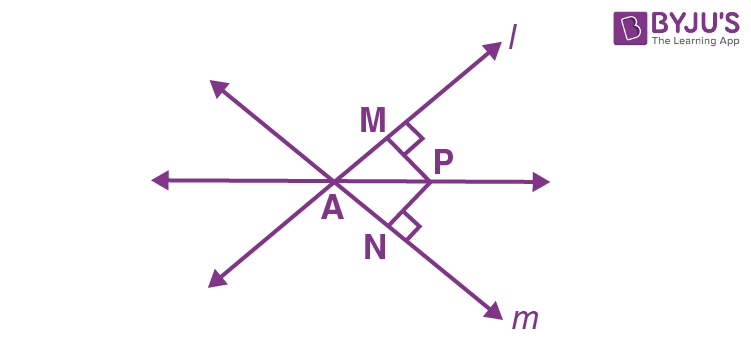
Example 7- In the figure given below, l and m are lines intersecting at A. P is a point equidistant from l and m. Prove that AP bisects the angle between l and m.
Example 8- The sides of a triangle are in the ratio 12:17:25 and its perimeter is 540 cm. Find the area of the triangle.
Example 9- Factorise:
(i) \(3x^{3} + \sqrt{3}x -2\)
(ii) \(\sqrt{2}x^{2} + 3x + \sqrt{2}\)
Example 10- If \(p^{2}+ 4q^{2}+ 9r^{2} = 2pq + 6qr + 3pr\), then prove that \(p^{3}+ 8q^{3}+ 27r^{3} = 18pqr\).
Example 11- Express \(0.\bar{3}\) as a rational number in the form \(\frac{p}{q}\), where p and q are integers and \(q \neq 0\).
Example 12- Find the product with the suitable identity \(\left ( x – \frac{1}{2} \right )\left ( x + \frac{1}{2} \right )\left ( x^{2} + \frac{1}{x^{2}} \right )\left ( x^{4} + \frac{1}{x^{4}} \right )\).
Example 13- If the two lines intersect each other then prove that vertically opposite angles are equal.
Example 14- Find the area of triangular park whose sides area of length 120m, 80m and 50m.
Example 15- If (3x-2) is a factor of \(3x^{3}+ x^{2} – 20x + 12\), find the other factors.
Example 16- Simplify \(\frac{\sqrt[2]{6}}{\sqrt{2}+\sqrt{3}} + \frac{\sqrt[6]{2}}{\sqrt{6}+\sqrt{3}} – \frac{\sqrt[8]{3}}{\sqrt{6}+\sqrt{2}}\)
Example 17- Cards marked with number 2 to 101 are placed in a box and mixed thoroughly. One card is drawn from this box. Find the probability that the number on the card-
(i) Multiple of 5
(ii) A number which is not a perfect square
(iii) A two digit number whose sum of digit is 9.
Example 18- Find the volume of the largest right circular cone that can be fitted in a cube whose edge is 21 cm.
Example 19- If the mean of the following data is 20.2, then find the value of p.
| X | 10 | 15 | 20 | 25 | 30 |
| f | 6 | 8 | p | 10 | 6 |
Example 20- A plastic box 1.5m long, 1.25m wide and 65 cm deep is to be made. It is to be open at the top. Ignoring the thickness of the plastic sheet, determine:
(i) the area of the sheet required for making the box.
(ii) the cost of sheet for it, if a sheet measuring 1\(m^{2}\) cost Rs. 20.
Example 21- If one side of a cyclic quadrilateral is produced, then the exterior angle is equal to the interior angle. Prove it.
Example 22- A hemisphere dome of a building needs to be painted. If the circumference of the base of the dome is 17.6 m, find the cost of painting it, given the cost of painting is Rs. 5 per 100 \(cm^{2}\).
To get more class-wise and chapter-wise important questions and answers, stay tuned with BYJU’S – The Learning App and download the app to learn the concepts quickly by exploring more videos.