Circles Class 9
Circles class 9 – The collection of all points equidistant from a fixed point in a plane is called a circle. Let us discuss in detail about the definitions and terminologies used in a concept of the circle.
Circles Class 9 Notes
- A plane is divided by the circle into 3 parts, namely, the interior and exterior of the circle and the circle itself.
- A chord is a line passing from one point to another on the circumference of a circle.
- Diameter is a chord that passes through the centre.
- The perimeter of a circle is known as the circumference.
- Chords equal in length subtend equal angles at centre. Similarly, the chords are equal if the angles subtended by chords are equal at the centre.
- The perpendicular drawn on a chord from centre bisects the chord. Similarly, the line is perpendicular if it is drawn from the centre to bisects the chord.
- Only one circle can pass through 3 non-collinear points.
- Chords equal in length are equidistant from the centre. Similarly, Chords are equal if they are equidistant from the centre.
- In a cyclic quadrilateral, the sum of pair of angles opposite to each other is 180 degree.
- Angles subtended by the same line segment are equal.
- If chords of a circle are equal in length, then the corresponding arcs will be congruent. Similarly, if arcs are congruent, then the corresponding chords will be equal.
Circles Class 9 Examples
Example 1:
An arc of a circle is given. Complete the circle.
Solution:
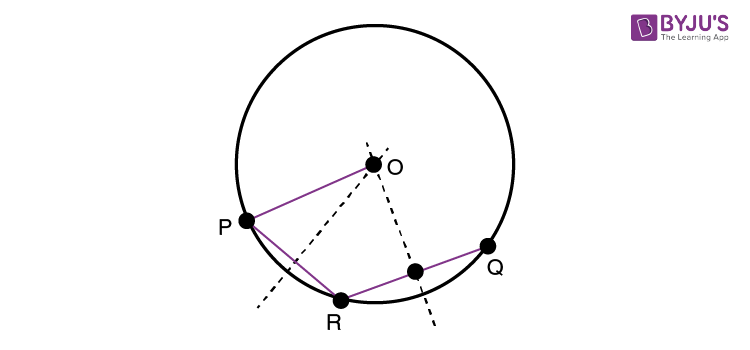
Let assume that PQ is the given arc of a circle. Now, we have to complete the circle for the given arc. It means that we need to find the radius and the centre point of a circle.
Now, take the point R on the circle, and join the points PR and RQ. Now, by using the theorem: “There is one and only one circle passing through the three given non-collinear points”. Now, construct a circle based on this theorem to find the centre and radius. After obtaining the radius and centre, complete the circle for the given arc.
Example 2:
Prove that the chords are equal if two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection.
Solution:
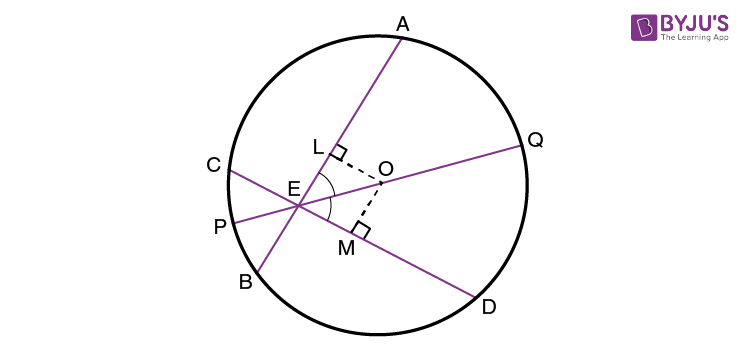
Given: AB and CD are the two chords of a circle with centre “O”. The intersection of these two chords is “E”. Now, PQ is the diameter of a circle, which passes through the point, such that ∠AEQ = ∠DEQ.
Now, we need to prove AB = CD. To prove this, draw the perpendiculars OL and OM on the chords AB and CD respectively.
By using the angle sum property of a triangle, we can write:
∠LOE = 180° – 90° – ∠LEO = 90° – ∠LEO
Therefore,
=90° – ∠AEQ = 90° – ∠DEQ
= 90° – ∠MEO = ∠MOE
From the triangles, OLE and OME,
∠LEO = ∠MEO
∠LOE = ∠MOE
EO = EO (Common)
Hence, ∆ OLE ≅ ∆ OME, Which means that OL = OM
Thus, the chord AB and CD are equal.
Hence, proved.
Example 3:
Two circles intersect at two points A and B, and AC and AD are the diameters of the circle. Show that the point B lies on the line segment DC.
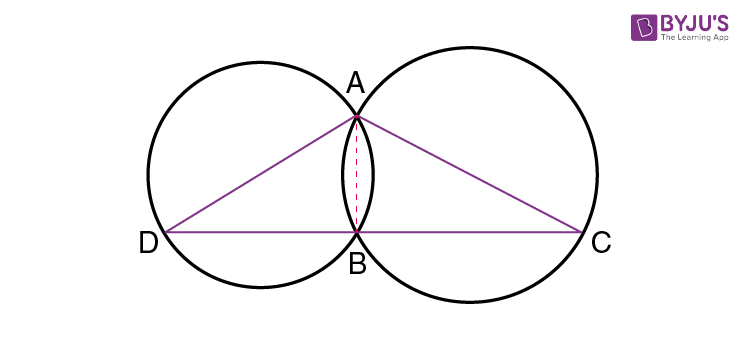
Solution:
From the given figure, join the points A and B.
Now, ∠ABD = 90° and ∠ABC = 90° (Angle in a semicircle)
Therefore, ∠ABD + ∠ABC = 90° + 90° = 180°
Now, DBC is a line. It means that point B lies in the line segment DC.
Hence, proved.
Practice Problems
- Prove that the segments of one chord are equal to corresponding segments of the other chord if two equal chords of a circle intersect within the circle.
- ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, then determine ∠ BCD. Also, if AB = BC, find ∠ECD.
- Show that a cyclic parallelogram is a rectangle.
To learn all the class-wise topics, download BYJU’S – The Learning App and watch personalized videos to learn with ease.