Percent errors indicate how big our errors are when we measure something in an analysis process. Smaller percent errors indicate that we are close to the accepted or original value. For example, a 1% error indicates that we got very close to the accepted value, while 48% means that we were quite a long way off from the true value. Measurement errors are often unavoidable due to certain reasons like hands can shake, material can be imprecise, or our instruments just might not have the capability to estimate exactly. Percent error formula will let us know how seriously these inevitable errors influenced our results.

Definition

Percent error is the difference between estimated value and the actual value in comparison to the actual value and is expressed as a percentage. In other words, the percent error is the relative error multiplied by 100.

Percent Error Formula

The formula for percent error is:

PE = (|Estimated value-Actual value|/ Actual value) × 100

Or

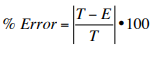
Here,

T = True or Actual value

E = Estimated value

How is the percent error calculated?

Below steps describe how to obtain the percent error in detail.

Step 1:Take the difference of one value from another. If we are ignoring the sign, the order does not matter. But we need to subtract the original value from the determined value if we are keeping negative signs. This value is “error.”

Step 2: Perform division operation for the error by the accurate or ideal value (not estimated or measured value). This results in a decimal number.

Step 3: Multiply it by 100 to transform a decimal number into a percentage.

Step 4: Add a percentage symbol (%) to represent percent error value.

Percent Error of Mean

Percent error mean or Mean percentage error is the average of all percent errors of the given model. The formula for mean percentage error is given by:

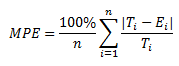
Here,

T_i = True or actual value of i^th quantity

E_i = Estimated value of i^th quantity

n = number of quantities in the model

The main disadvantage of this measure is that it is undefined, whenever a single actual value is zero.

Read more:

How To Calculate Percentage

Percentage Increase Decrease

Percent Error Example

The below examples help in better understanding of percent error.

Example 1:

A boy measured the area of a rectangle plot to be 468 cm². But the actual area of the plot has been recorded as 470 cm². Calculate the percent error of his measurement.

Solution:

Given,

Measured area value = 468 cm²

Actual area value = 470 cm²

Steps of calculation:

Step 1: Subtract one value from another; 468 – 470 = -2

By ignoring the negative sign, the difference is 2, which is the error.

Step 2: Divide the error by actual value; 2/470 = 0.0042531

Multiply this value by 100; 0.0042531 × 100 = 0.42% (expressing it in two decimal points) Hence, 0.42% is the percent error.

Example 2:

A person started a new business on 1st January. Based on the demand in that particular area, he expected a certain number of customers who can visit his shop per month. The following table gives the information on the number of visitors for the shop during the first quarter.

Find the mean percent error for the above data.

Solution:

Mean percent error = (11.11% + 20% + 5%)/ 3

= 36.11%/3

=12.0367% (approx)

Note:

The purpose of calculating the percent error is to analyse how close the measured value is to an actual value. It is part of a comprehensive error analysis. In most of the fields, percent error is always expressed as a positive number whereas in others, it is correct to have either a positive or negative value. The idea of keeping the sign is to determine whether recorded values consistently fall above or below expected values.