Proper Fractions
Before getting into the proper fractions, let us know what a fraction is? When is the fraction called the proper fraction? Fraction is defined as the part of the whole thing. Mathematically, a fraction is defined as the ratio of two numbers. The general form of a fraction is a/b such that b ≠ 0 and a, b are whole numbers; a is the numerator, and b is the denominator. Fractions are categorized into various types based on the numerical value of numerator and denominator. Also, a fraction is called a proper fraction if the denominator is greater than the numerator. If the numerator is greater than the denominator, then it is an improper fraction.
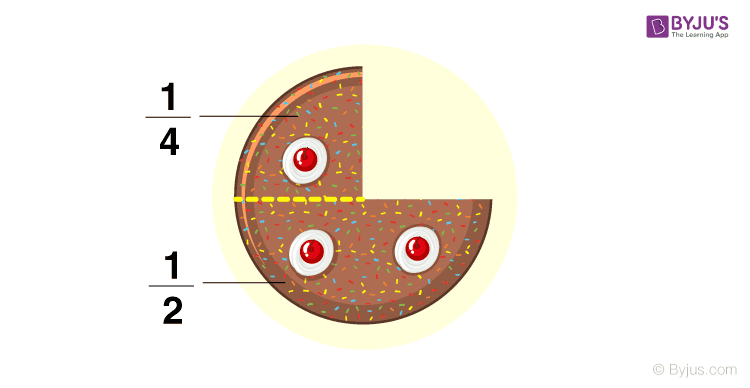
The figure above shows the fractions which are also proper fractions since the denominator is greater than the numerator.
Let’s learn in detail about What are Proper fractions? How to identify the proper fraction, how to work with proper fractions in different situations along with examples now.
Let’s have a look at the definition of proper fractions.
Proper Fractions Definition
When the numerator of a fraction is less than the denominator, it is called a Proper fraction. That means, for proper fractions, denominators will be always greater than the numerator.
Fractions are called Proper Fractions when:
Numerator < Denominator
(Or)
Denominator > Numerator
Go through the meaning of a fraction, denominator and numerator along with the example given below. This will help you in understanding the exact meaning of proper fractions.
- If you want to describe a part of a whole, it is called a Fraction.
- Denominator – The number on the bottom of the fraction and it shows the number of equal parts, where the whole is divided into.
- Numerator – The numerator is the number on the top of the fraction, and it shows the number of the parts we are considering.
- Example, in the fraction 5/6, it shows “5 of 6 equal parts.” 5 is the numerator, and 6 is the denominator.
Example of a Proper Fraction:
\(\frac{3}{5}\) where 3 is a numerator less than 5, which is the denominator.
Few more Proper Fraction examples are :
\(\frac{1}{9} , \frac{2}{7}, \frac{4}{9}\).Note: In all the above examples, the number on the top (numerator) is smaller than the number at the bottom(denominator).
So, basically, it is a way to divide or cut any object in smaller parts. Example, if you divide a bar of chocolate into two equal parts, it would be called two halves.
It can be denoted mathematically as
\(\frac{1}{2} +\frac{1}{2}= 1\)This expression is called a Fraction. You may divide the chocolate bar into more pieces too.
| Also, it is important to note that proper fractions are always less than 1. In other words, we can say that all proper fractions are less than 1. That means, when we convert the given proper fraction into decimal we always get the value which is less than 1. |
Types of fractions:
There are 3 types of fractions, and an overview of them is given below:
| Types of Fractions | Proper Fractions / Common Fractions | Improper Fractions | Mixed Fractions |
| Property | In this, the numerator is smaller than the denominator. | In this, the numerator is larger or equal than the denominator. | It’s a combination of a whole number and a proper fraction. |
| Example | \(\frac{2}{3}\) | \(\frac{2}{1} or \frac{5}{5}\) | \(5\frac{1}{2}\) |
Point to know – If the numerator and denominator of a fraction are multiplied by the same number, its value doesn’t change.
Proper Fractions Examples
Let’s Solve a few problems on Proper fractions:
| Question | Answer |
| Is \(\frac{1}{2}\) a proper fraction? | Yes, It is a proper fraction because the numerator 1 in this fraction is less than the denominator 2. |
| Is \(\frac{4}{2}\) a proper fraction? | No, It is not a proper fraction because the numerator 4 in this fraction is more than the denominator 2. It is an improper fraction. |
| Is \(\frac{9}{8}\) a proper fraction? | No, It is not a proper fraction because the numerator 9 in this fraction is more than the denominator 8. It is an improper fraction. |
| Is \(\frac{6}{5}\) a proper fraction? | No, It is not a proper fraction because the numerator 6 in this fraction is more than the denominator 5. It is an improper fraction. |
| Is \(\frac{5}{9}\) a proper fraction? | Yes, It is a proper fraction because the numerator 5 in this fraction is less than the denominator 9. |
How to Solve Proper Fractions?
As we know numbers can undergo different arithmetic operations such as addition, subtraction, multiplication and division. Similarly, we can perform these operations on proper fractions too. Let us learn how to solve proper fractions involving arithmetic operations.
Addition and subtraction of Proper Fractions
In this section, you will learn How to add Proper fractions and how to subtract proper fractions with the help of examples.
Example 1: Add 2/4 and 3/4.
Solution:
(2/4) + (3/4)
Here, the denominators are the same.
(2/4) + (3/4)= (2 + 3)/4
= 5/4
Example 2: Subtract 6/10 from 3/4.
Solution:
(3/4) – (6/10)
Here, the denominators are not equal.
So, let us make the denominators equal.
LCM of 4 and 10 = 20
Thus,
(3/4) = (3/4) × (5/5) = 15/20
(6/10) = (6/10) × (2/2) = 12/20
Therefore, (3/4) – (6/10) = (15/20) – (12/20) = (15 – 12)/20 = 3/20
In the same way, we multiply and divide given proper fractions.
Learn how to simplify fractions here.
Note: The addition of two proper fractions may also give the improper fraction as the result and the subtraction of two proper fractions may result in the negative value too.
To learn more about fractions and operations on fractions, visit www.byjus.com. Also, download BYJU’S – The Learning App for personalised videos.