Properties of Triangle
All the properties of a triangle are based on its sides and angles. By the definition of triangle, we know that, it is a closed polygon that consists of three sides and three vertices. Also, the sum of all three internal angles of a triangle equal to 180°.
Depending upon the length of sides and measure of angles, the triangles are classified into different types of triangles. Triangle is an important concept which is taught in most of the classes like Class 7, Class 8, Class 9, Class 10 and in Class 11. You will learn the properties of triangles here along with its definitions, types and its significance in Maths.
In the beginning, we start from understanding the shape of triangles, its types and properties, theorems based on it such as Pythagoras theorem, etc. In higher classes, we deal with trigonometry, where the right-angled triangle is the base of the concept. Let us learn here some of the fundamentals of the triangle by knowing its properties.
Also check: Angle Sum Property Of A Triangle
Types of Triangle
| Based on the Sides | Based on the Angles |
| Scalene Triangle | Acute angled Triangle |
| Isosceles Triangle | Right angle Triangle |
| Equilateral Triangle | Obtuse-angled Triangle |
So before, discussing the properties of triangles, let us discuss types of triangles given above.
Scalene Triangle: All the sides and angles are unequal.
Isosceles Triangle: It has two equal sides. Also, the angles opposite these equal sides are equal.
Equilateral Triangle: All the sides are equal and all the three angles equal to 60°.
Acute Angled Triangle: A triangle having all its angles less than 90°.
Right Angled Triangle: A triangle having one of the three angles exactly 90°.
Obtuse Angled Triangle: A triangle having one of the three angles more than 90°.
Triangle Properties
The properties of the triangle are:
- The sum of all the angles of a triangle (of all types) is equal to 180°.
- The sum of the length of the two sides of a triangle is greater than the length of the third side.
- In the same way, the difference between the two sides of a triangle is less than the length of the third side.
- The side opposite the greater angle is the longest side of all the three sides of a triangle.
- The exterior angle of a triangle is always equal to the sum of the interior opposite angles. This property of a triangle is called an exterior angle property.
- Two triangles are said to be similar if their corresponding angles of both triangles are congruent and the lengths of their sides are proportional.
- Area of a triangle = ½ × Base × Height
- The perimeter of a triangle = sum of all its three sides
Triangle Formula
- Area of a triangle is the region occupied by a triangle in a two-dimensional plane. The dimension of the area is square units. The formula for area is given by;
Area = 1/2 x Base x Height
- The perimeter of a triangle is the length of the outer boundary of a triangle. To find the perimeter of a triangle we need to add the length of the sides of the triangle.
P = a + b + c
- Semi-perimeter of a triangle is half of the perimeter of the triangle. It is represented by s.
s = (a + b + c)/2
where a, b and c are the sides of the triangle.
- By Heron’s formula, the area of the triangle is given by:
A = √[s(s – a)(s – b)(s – c)]
where ‘s’ is the semi-perimeter of the triangle.
- By the Pythagorean theorem, the hypotenuse of a right-angled triangle can be calculated by the formula:
Hypotenuse2 = Base2 + Perpendicular2
Also check:
Solved Examples
Example 1: If an equilateral triangle has lengths of sides as 5 cm and perpendicular is drawn from the vertex to the base of the triangle, then find its area and perimeter.
Solution: Given, side of the equilateral triangle, say AB = BC = CD = 5 cm
If we draw a perpendicular from the vertex of an equilateral triangle, A to the base at point O, it divides the base into two equal sides.
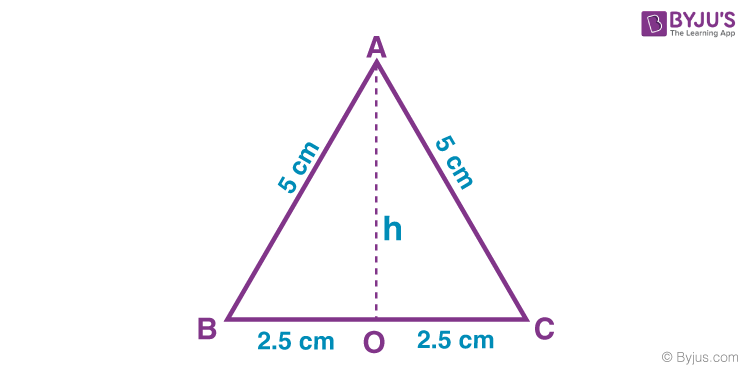
Such that, BO = OC = 2.5 cm
Now, the area of triangle = ½ × Base × Height
To find the height of the triangle, AOB, we have to use Pythagoras theorem.
That is, Hypotenuse2 = Base2 + Perpendicular2
Or Perpendicular = \(\sqrt{Hypotenuse^2-Base^2}\)
Therefore, OA = \(\sqrt{AB^2-OB^2}\)
Or OA = \(\sqrt{5^2-2.5^2}\)
OA = \(\sqrt{25-6.25} = \sqrt{18.75}\)
Area of triangle ABC = ½ × BC × OA
= ½ × 5 × \(\sqrt{18.75}\) = 2.5 × 4.33
Area of triangle ABC = 10.825 cm2
Perimeter of triangle ABC = sum of all its three sides
= 5 + 5 + 5 cm
= 15 cm
Example 2: If the sides of a triangle are given by 3 cm, 4 cm and 5 cm, where the base is 4cm and the altitude of the triangle is 3.2 cm, then find the area and perimeter of the triangle.
Solution: Let the given sides of the triangle be:
a = 3 cm, b = 4 cm and c = 5 cm
Altitude is the height of the triangle = 3.2 cm
By the formula of area of the triangle, we know;
Area = 1/2 x base x height
A = (1/2) x 4 x 3.2
A = 6.4 sq.cm.
Now, the perimeter of the triangle is given by;
P = a + b + c
P = 3 + 4 + 5
P = 12 cm.
Learn more about different interesting topics of geometry here at BYJU’S. Also, download the BYJU’S app to get a visual of such figures and understand the concepts in a better and creative way.
Frequently Asked Questions – FAQs
What are the five properties of triangles?
It has three sides, three vertices and three angles.
Sum of all three angles equal to 180 degrees
Sum of the length of any two sides of a triangle is always greater than the third side
Perimeter of the triangle is equal to the sum of all three sides
Area of triangle is equal to half of the product of base and height
What are the types of triangles and their properties?
Scalene triangle: all three sides are of different length
Isosceles triangle: Any two sides are of equal length
Equilateral triangle: All three sides are of equal length
Acute-angled triangle: Any one of the three angles measures less than 90 degrees
Obtuse-angled triangle: Any one of the three angles measures more than 90 degrees
Right-angled triangle: Any one angle is exactly equal to 90 degrees
What do we mean by triangle?
What is the angle sum property of triangles?
∠A + ∠B + ∠C = 180 degrees