Quadrilateral
A quadrilateral is a closed shape and a type of polygon that has four sides, four vertices and four angles. It is formed by joining four non-collinear points. The sum of interior angles of quadrilaterals is always equal to 360 degrees.
The word quadrilateral is derived from the Latin words ‘Quadra’ which means four and ‘Latus’ means ‘sides’. It is not necessary that all the four sides of a quadrilateral are equal in length. Hence, we can have different types of quadrilaterals based on sides and angles. Let us more interesting facts about quadrilaterals in this article.
| Table of Contents: |
What is a Quadrilateral?
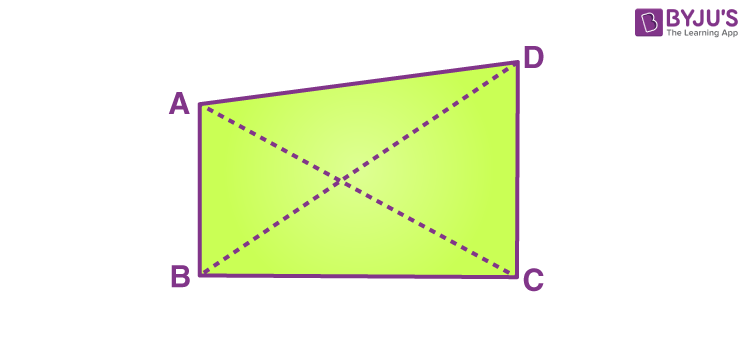
A quadrilateral is a plane figure that has four sides or edges, and also has four corners or vertices. The angles are present at the four vertices or corners of the quadrilateral. If ABCD is a quadrilateral then angles at the vertices are ∠A, ∠B, ∠C and ∠D. The sides of a quadrilateral are AB, BC, CD and DA.
If we join the opposite vertices of the quadrilateral, we get the diagonals. In the below figure AC and BD are the diagonals of quadrilateral ABCD.
Quadrilaterals will typically be of standard shapes with four sides like rectangle, square, trapezoid, and kite or irregular and uncharacterized as shown below:

Let’s have a look at the table below to understand what quadrilateral is.
| Quadrilateral | Two-dimensional plane figure enclosed by 4 line segments
Or A polygon with 4 edges and 4 vertices |
| Number of sides | 4 |
| Number of vertices | 4 |
| Number of diagonals | 2 |
| Sum of all interior angles | 360 degrees |
| Sum of all exterior angles | 360 degrees |
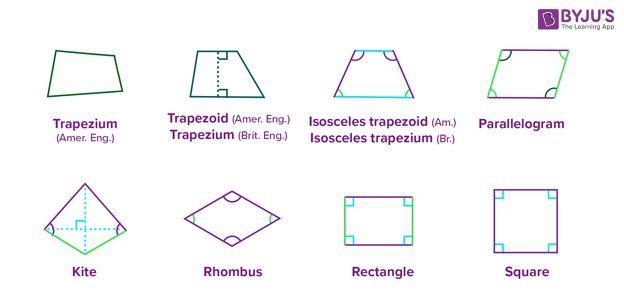
Types of Quadrilaterals
The types of quadrilaterals are defined based on the measure of the angles and lengths of their sides. As the word ‘Quad’ means four, all these types of a quadrilateral have four sides, and the sum of angles of these shapes is 360 degrees. The list of types of quadrilaterals are:
-
- Trapezium
- Parallelogram
- Squares
- Rectangle
- Rhombus
- Kite
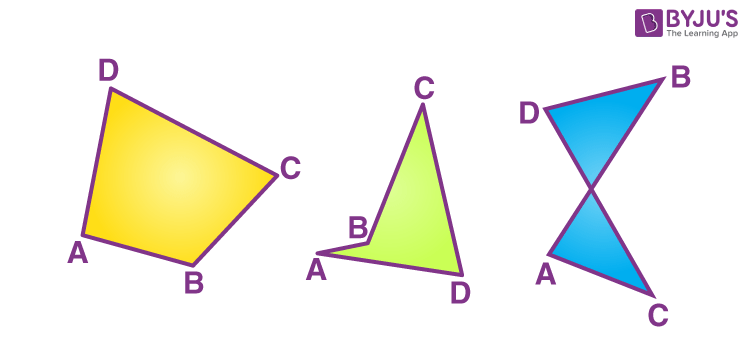
Convex, Concave and Intersecting Quadrilaterals
Another way to classify the types of quadrilaterals are:
- Convex Quadrilaterals: Both the diagonals of a quadrilateral are completely contained within a figure.
- Concave Quadrilaterals: At least one of the diagonals lies partly or entirely outside of the figure.
- Intersecting Quadrilaterals: Intersecting quadrilaterals are not simple quadrilaterals in which the pair of non-adjacent sides intersect. These kinds of quadrilaterals are known as self-intersecting or crossed quadrilaterals
Below are the examples of convex, concave and intersecting quadrilaterals.
Properties of Quadrilaterals
Let us understand in a better way with the help of an example:
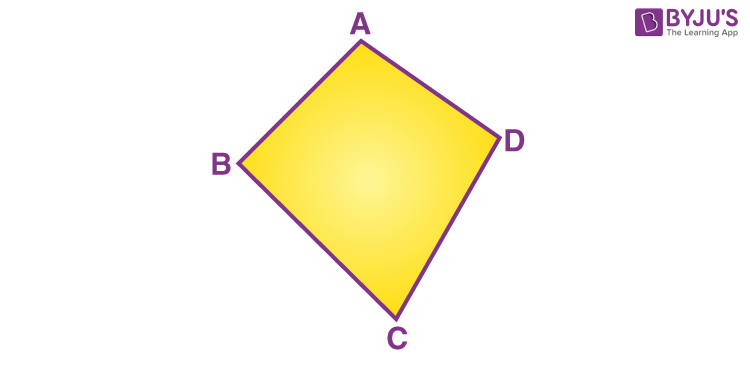
- It has four sides: AB, BC, CD, and DA
- It has four vertices: Points A, B, C, and D
- It has four angles: ∠ABC, ∠BCD, ∠CDA, and ∠DAB
- ∠A and ∠B are adjacent angles
- ∠A and ∠C are the opposite angles
- AB and CD are the opposite sides
- AB and BC are the adjacent sides
A quadrilateral is a 4-sided plane figure. Below are some important properties of quadrilaterals :
- Every quadrilateral has 4 vertices, 4 angles, and 4 sides
- The total of its interior angles = 360 degrees
Square Properties
- All the sides of the square are of equal measure
- The sides are parallel to each other
- All the interior angles of a square are at 90 degrees (i.e., right angle)
- The diagonals of a square perpendicular bisect each other
To learn more about square, click here.
Rectangle Properties
- The opposite sides of a rectangle are of equal length
- The opposite sides are parallel to each other
- All the interior angles of a rectangle are 90 degrees.
- The diagonals of a rectangle bisect each other.
To understand more about rectangle, visit here.
Rhombus Properties
- All the four sides of a rhombus are of the same measure
- The opposite sides of the rhombus are parallel to each other
- The opposite angles are of the same measure
- The sum of any two adjacent angles of a rhombus is equal to 180 degrees
- The diagonals perpendicularly bisect each other
Learn in detail about rhombus here.
Parallelogram Properties
- The opposite side of the parallelogram are of the same length
- The opposite sides are parallel to each other
- The diagonals of a parallelogram bisect each other
- The opposite angles are of equal measure
- The sum of two adjacent angles of a parallelogram is equal to 180 degrees
Also, check: Parallelogram
Properties of Trapezium
- Only one pair of the opposite side of a trapezium is parallel to each other
- The two adjacent sides of a trapezium are supplementary (180 degrees)
- The diagonals of a trapezium bisect each other in the same ratio
Click here to learn the definition and formulas related to trapezium.
Properties of Kite
- The pair of adjacent sides of a kite are of the same length
- The largest diagonal of a kite bisect the smallest diagonal
- Only one pair of opposite angles are of the same measure.
A glance at the Quadrilateral Properties
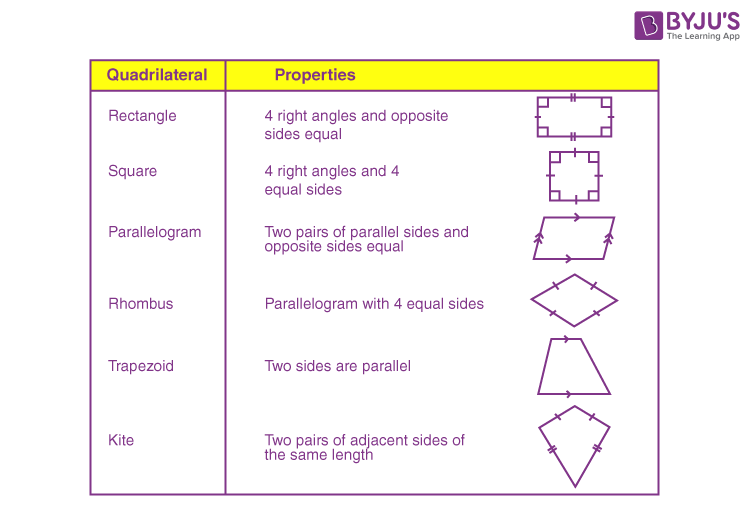
Sides and Angles of Quadrilaterals
| Sides and angles | Square | Rectangle | Rhombus | Parallelogram | Trapezium |
| All sides are equal | Yes | No | Yes | No | No |
| Opposite sides are parallel | Yes | Yes | Yes | Yes | Yes |
| Opposite sides are equal | Yes | Yes | Yes | Yes | No |
| All the angles are of the same measure | Yes | Yes | No | No | No |
| Opposite angles are of equal measure | Yes | Yes | Yes | Yes | No |
| Diagonals bisect each other | Yes | Yes | Yes | Yes | No |
| Two adjacent angles are supplementary | Yes | Yes | Yes | Yes | No |
Quadrilateral Formulas
There are two basic formulas for quadrilaterals, that are:
- Area
- Perimeter
Area of Quadrilateral
The area of the quadrilateral is the total space occupied by the figure. The area formula for the different quadrilaterals are given below:
| Area of a Parallelogram | Base x Height |
| Area of a Rectangle | Length x Width |
| Area of a Square | Side x Side |
| Area of a Rhombus | (1/2) x Diagonal 1 x Diagonal 2 |
| Area of a Kite | 1/2 x Diagonal 1 x Diagonal 2 |
Perimeter of Quadrilateral
Perimeter is the total distance covered by the boundary of a 2d shape. Since we know the quadrilateral has four sides, therefore, the perimeter of any quadrilateral will be equal to the sum of the length of all four sides. If ABCD is a quadrilateral then, the perimeter of ABCD is:
Perimeter = AB + BC + CD + AD
| Quadrilateral Name | Perimeter |
| Square | 4 x Side |
| Rectangle | 2(Length + Breadth) |
| Parallelogram | 2(Base + Side) |
| Rhombus | 4 x Side |
| Kite | 2 (a + b), a and b are adjacent pairs |
Important Facts of Quadrilateral
- A quadrilateral is a trapezoid or a trapezium if 2 of its sides are parallel to each other.
- A quadrilateral is a parallelogram if 2 pairs of sides parallel to each other.
- Squares and Rectangles are special types of parallelograms. Below are some special properties.– All internal angles are of “right angle” (90 degrees).– Each figure contains 4 right angles.– Sides of a square are of the same length (all sides are congruent) – Opposite sides of a rectangle are the same.– Opposite sides of a rectangle and square are parallel.
- A quadrilateral is a rhombus, if
- All the sides are of equal length-specified 2 pairs of sides are parallel to each other.
- A kite is a special sort of quadrilateral, in which 2 pairs of adjacent sides are equal to each other.
Quadrilaterals Solved Examples
Example 1: What is the base of a rhombus, if its area is 40 square units and the height is 8 units?
Solution:
Given,
Area = 40 square units
Height = 8 units
Area of rhombus = Base × Height
40 = Base × 8
Base = 40/8 = 5 units
Example 2: If 15 metres and 6 metres are diagonal lengths of a kite, then what is its area?
Solution: Given, diagonal 1 = 15 metre and diagonal 2 = 6 metre. So, the area is simply calculated as, (1/2)(15×6) = 45 m2.
Example 3: Find the perimeter of the quadrilateral with sides 5 cm, 7 cm, 9 cm and 11 cm.
Solution: Given, sides of a quadrilateral are 5 cm, 7 cm, 9 cm and 11 cm.
Therefore, perimeter of quadrilateral is:
P = 5 cm + 7 cm + 9 cm + 11 cm = 32 cm
Example 4: The perimeter of the quadrilateral is 50 cm and the lengths of the three sides are 9 cm, 13 cm and 17 cm. Find the missing side of the quadrilateral.
Solution: Let the unknown side of the quadrilateral = x
Given, Perimeter of the quadrilateral = 50 cm
The lengths of other three sides are 9 cm, 13 cm and 17 cm
As we know,
Perimeter = sum of all the four sides.
50 = 9 cm + 13 cm + 17 cm + x
50 = 39 + x
x = 50 – 39
x = 11
Therefore, the fourth side of quadrilateral = 11 cm
Practice Questions on Quadrilaterals
- What is the area of a square with a side length equal to 13 cm?
- What is the perimeter of rectangle if length = 14cm and breadth = 10 cm?
- The angles of a quadrilateral are in the ratio 3 : 5 : 9 : 13. Find all the angles of the quadrilateral.
Related Articles
To get more such Math lessons in a simple and easy-to-understand way, register at BYJU’S and score well in your exams.
Frequently Asked Questions
What are Quadrilaterals and their types?
A quadrilateral can be defined as a plane figure having 4 sides. There are mainly 6 types of quadrilaterals which are:
- Trapezium
- Parallelogram
- Rectangle
- Rhombus
- Square
- Kite
Apart from these 6 types, a quadrilateral can also be classified as:
- Concave quadrilaterals
- Convex quadrilaterals
- Intersecting quadrilaterals
What is a convex and concave quadrilateral?
A convex quadrilateral can be defined as a quadrilateral whose both the diagonals are completely contained within the figure. On the other hand, a concave quadrilateral is a quadrilateral which is having at least one diagonal that lies partly or entirely outside of the figure.
What is the sum of the interior angles of a quadrilateral?
The sum of all the interior angles of a quadrilateral is 360°.
What are the three attributes of a quadrilateral?
The three important attributes of a quadrilateral are:
Four sides
Four Vertices
The sum of the interior angles should be equal to 360 degrees.
How to find the perimeter of a quadrilateral?
The perimeter of a quadrilateral can be determined by adding the side length of all four sides.