Solids
In Geometry, the shape or the figure that has three (even higher) dimensions, are known as solids or three-dimensional shapes. The study of the properties, volume and surface area of three-dimensional shapes is called Solid Geometry. Let us go ahead and focus more on the study of geometrical solids.
Geometric Shapes
The geometrical figures classified based on the dimensions are as follows:
- Zero dimensional shape – A point.
- One dimensional shape – A line that has a length as its dimension.
- Two-dimensional shapes – A figure that has length and breadth as two dimensions. For example – square, triangle, rectangle, parallelogram, trapezoid, rhombus, quadrilateral, polygon, circle etc.
- Three-dimensional shapes – An object with length, breadth and height as three dimensions. For example – cube, cuboid, cone, cylinder, sphere, pyramid, prism etc.
- Higher-dimensional shapes – There are few shapes expressed in dimensions higher than 3, but we usually do not study them in middle-level mathematics.
What are solids?
In geometry, there are various types of solids. Solids are three-dimensional shapes because they have three dimensions such as length, breadth and height. The bodies which occupy space are called solids.
Solid or 3D shapes properties
Solids are classified in terms of their properties. To analyze characteristics and properties of 3-D geometric shapes, count the number of faces, edges, and vertices in various geometric solids. Let us discuss the properties and formulas for the different solid shapes.
| Solid Shape | Figure | Property | Volume Formula
(Cubic Units) |
Surface Area Formula
(Square Units) |
| Cube | 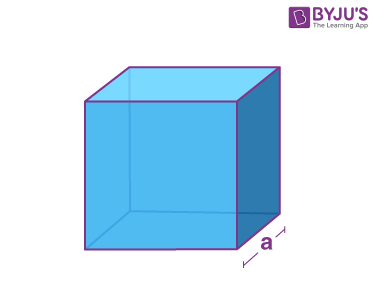 |
Face – square (6)
vertices – 8 Edges – 12 |
a3 | 6a2 |
| Cuboid | 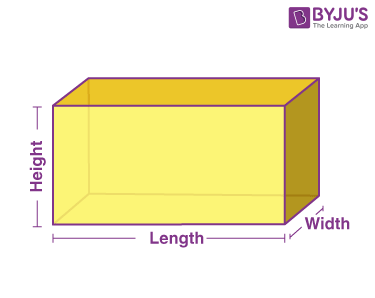 |
Face – Rectangle (6)
vertices – 8 Edges – 12 |
l × b × h | 2(lb+lh+hb) |
| Sphere | 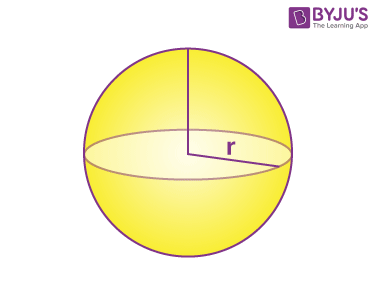 |
Curved surface = 1
Edges = 0 Vertices = 0 |
(4/3)πr3 | 4πr2 |
| Cylinder | 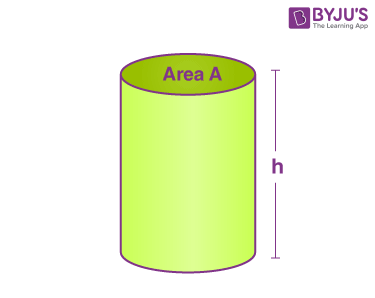 |
Flat Surface = 2
Curved Surface = 1 Face = 3 Edges =2 Vertices =0 |
πr2h | 2πr(r+h) |
| Cone | 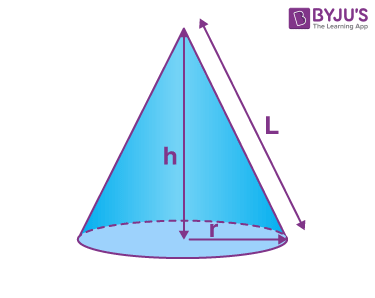 |
Flat Surface = 1
Curved Surface = 1 Face = 2 Edges = 1 Vertices =1 |
(⅓)πr2h | πr(r+l) |
Solids Examples
Question 1:
Find the volume and surface area of a cube whose side is 5 cm.
Solution:
Side, a = 5 cm
The volume of a cube formula is:
The volume of a cube = a3 cubic units
V = 53
V = 5 × 5 × 5
V =125 cm3
Therefore, the volume of a cube is 125 cubic centimetre
The surface area of a cube = 6a2 square units
SA = 6(5)2 cm2
SA = 6(25)
SA = 150 cm2
Therefore, the surface area of a cube is 150 square centimetre
Question 2:
Find the volume of the sphere of radius 7 cm.
Solution:
Given radius of the sphere = r = 7 cm
Volume of sphere = 4/3 πr3
= (4/3) × (22/7) × 7 × 7 × 7
= 4 × 22 × 7 × 7
= 4312 cm3
Question 3:
Find the total surface area of a cuboid of dimensions 8 cm × 5 cm × 7 cm.
Solution:
Given dimensions of a cuboid: 8 cm × 5 cm × 7 cm
That means, length = l = 8 cm
Breadth = b = 5 cm
Height = h = 7 cm
Total surface area of a cuboid = 2(lb + bh + hl)
= 2[8(5) + 5(7) + 7(8)]
= 2(40 + 35 + 56)
= 2 × 131
= 262 cm2
Register with BYJU’S – The Learning App and also download the app to explore engaging videos.