Solving Linear Inequalities
Solving linear inequalities by the graphical method is the easy way to find the solutions for linear equations. To solve a linear equation in one variable is simple, where we need to plot the value in a number line. But for two-variable cases, we have to plot the graph in an x-y plane. In linear inequality, a linear function is involved. A mathematical expression containing equal-to (=) symbol is known as an equation. The equality symbol signifies that the right-hand side of the expression is equal to the left-hand side of the expression. If two mathematical expressions contain symbols like ‘<’(less than), ‘>’ (greater than), ‘≤’(less than or equal to) or ‘≥’ (greater than or equal to), they are called inequalities.
For example,
Statement 1 – Neeta is 15 years old.
The equality symbol can be mathematically expressed as x = 15.
Statement 2 – Now if I say Neeta’s age is at least 15 years, then this can be expressed as x≥15.
Thus Statement 1 is equation and Statement 2 is inequality.
Let’s learn about solving inequalities in two variables.
Solving Linear Inequalities
Let us now discuss the method of solving inequalities graphically. The graph of a linear equation is a straight line and any point in the Cartesian plane with respect to that will lie on either side of the line. Let us consider the expression ax + by for a linear equation in two variables. The following inequalities can be framed using this expression.
1. ax + by < c
2. ax + by ≤ c
3. ax + by > c
4. ax + by ≥ c
For solving these inequalities consider the line ax + by = c, a≠ 0 and b ≠ 0. The graph of this line is as shown below.
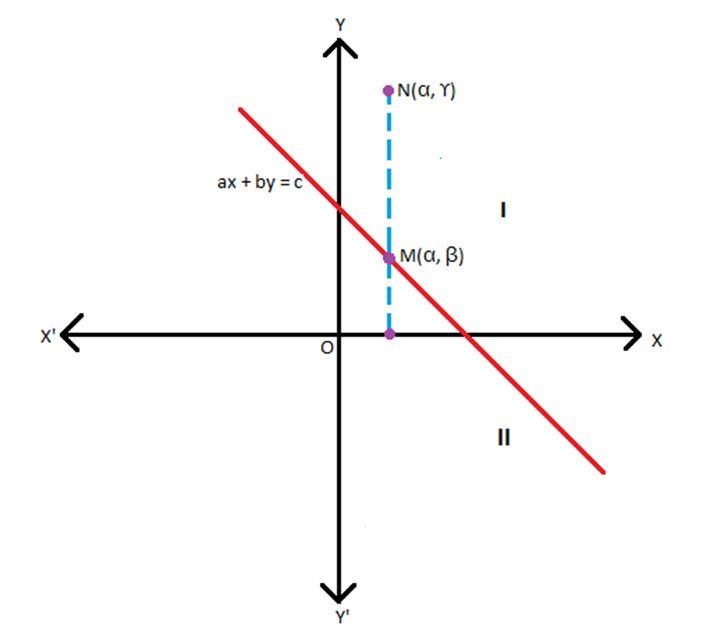
The graph of the line divides the Cartesian plane into two halves. All the points (x, y) lying on the line ax + by = c satisfy the equation i.e., both sides of the equation are balanced. The point (α, β) lying on the line ax + by = c represents a solution to the line. Thus, aα + bβ = c.
Now consider a point N (α, ϒ) lying in the upper half of the plane. It is pretty obvious from the graph that ϒ >β. Also, since the graph is represented by a straight line, it implies b>0 or else the equation ax + by = c would merely represent a point.
⇒bϒ> bβ
⇒aα + bϒ > aα + bβ (Adding aα on both sides)
⇒aα + bϒ> c
This inequality signifies that any point Q(α, ϒ) lying above or in the upper half of the plane or the region indicated by I formed by the line ax + by = c would satisfy the inequality ax + by > c.
Linear Inequalities Graphing
For solving inequalities mentioned above, we graph the linear expression and make the following conclusions about the inequality.
ax + by < c
The region lying below the line ax + by = c or the region marked II consists of all those points that would satisfy the inequality ax + by < c. Region II is, therefore, the solution region for the inequality of the type ax + by < c. Since the solution region excludes the line ax + by = c, therefore the line is dotted.
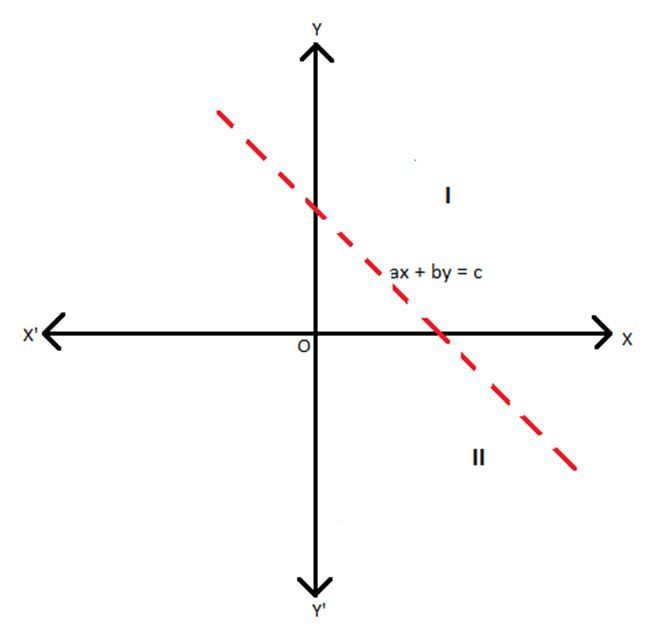
ax + by ≤ c
The region lying below and including the line ax + by = c or the region marked II consists of all those points that would satisfy the inequality ax + by ≤ c. Region II is, therefore, the solution region for the inequality of the type ax + by ≤ c.
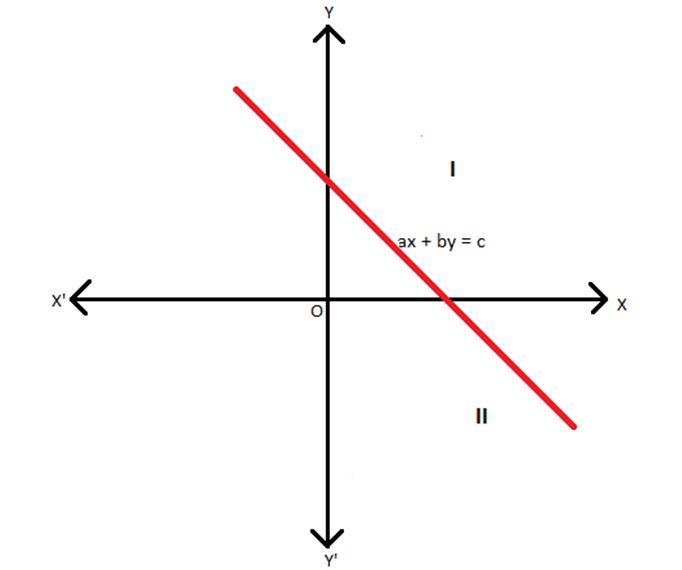
ax + by > c
The region lying in the upper half of the line ax + by = c or the region marked I consist of all those points that would satisfy the inequality ax + by > c. Region I is, therefore, the solution region for the inequality of the type ax + by > c. Since the solution region excludes the line ax + by = c, therefore the line is dotted.
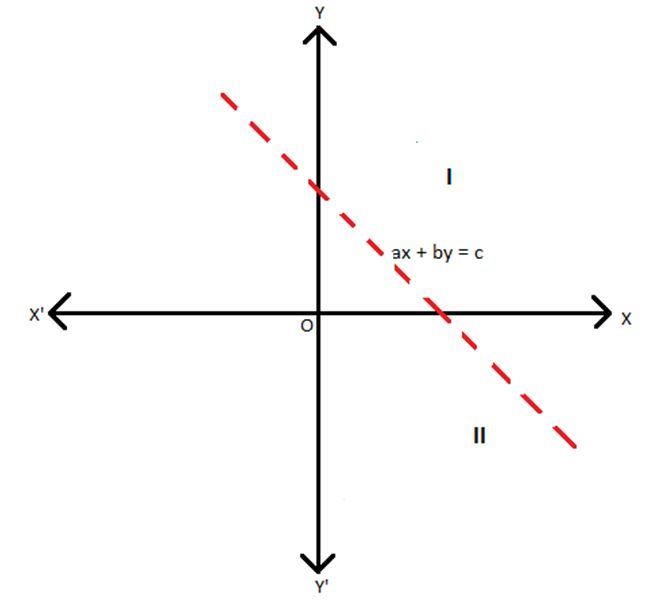
ax + by ≥ c
The region lying below and including the line ax + by = c or the region marked I consist of all those points that would satisfy the inequality ax + by ≥ c. Region I is, therefore, the solution region for the inequality of the type ax + by ≥ c.

Solving Linear Inequalities of One Variable
Solving linear inequalities of one variable involves various arithmetic operations such as addition, subtraction, multiplication and division. Also, the solution of the given inequality can be represented on the number line.
Solving Linear Inequalities of Two Variables
Graphical method is an essential tool for solving linear inequalities in two variables. In this case, the given inequalities are solved separately for two variables such as for x and y. Then, by combining the solutions, the graph of the given inequality will be obtained.
Solving Inequalities With Fractions
Solving inequalities with fractions is quite similar to solving inequalities of one variable. That means, the basic arithmetic operations are used here also to reduce the fractions into integers.
Let’s have a look at the examples given below for better understanding of all the three cases mentioned above.
Video Lesson
Fundamentals of Inequalities

Solving Linear Inequalities Examples
Example 1: Solve -2(x+3)<10
Solution: Given, -2(x+3)<10
Divide both the sides by 2, we get;
-(x+3)<5
-x-3<5
Add 3 both the sides
-x-3+3 < 5+3
-x < 8
Divide by -1 both the sides
-x/-1 < 8/-1
x>-8

Hence, the solution is x > -8.
Example 2: Solve: (3/4)x – (1/4) ≥ -⅛
Solution:
(3/4)x – (1/4) ≥ -1/8
Multiply both sides of the inequality by 8,
8 [(3/4)x – (1/4)] ≥ 8(-1/8)
6x – 2 ≥ – 1
Adding 2 on both sides,
6x -2 + 2 ≥ – 1 + 2
6x ≥ 1
Dividing by 6 on both sides,
x ≥ 1\6
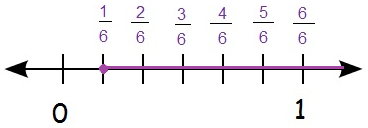
Thus, the solution is x ≥ ⅙.
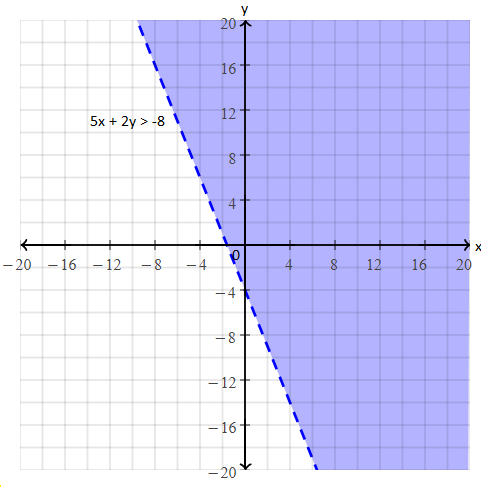
Example 3: Represent the solution of the linear inequality 5x + 2y > -8 graphically.
Solution: Given,
5x + 2y > -8
Solving for x:
5x + 2y > -8
Adding -2y on both sides,
5x + 2y – 2y > -8 – 2y
5x > -8 – 2y
Dividing by 5 on both sides,
x > (-2/5)y – 8/5
Solving for y:
5x + 2y > -8
Subtracting 5x from both sides,
5x + 2y – 5x > -8 – 5x
2y > -5x – 8
Dividing both sides of the inequality by 2,
y > (-5/2)x – 4
Graph:
To learn more about solving inequalities, download BYJU’S- The Learning App.