Matrix is one of the most commonly used elements in linear algebra. Matrix is the rectangular arrangement of numbers/elements/objects. The horizontal arrangement is called the row and the vertical arrangement is the column of a matrix. The order of a matrix is determined by the number of rows by columns. Suppose a matrix has 2 rows and 3 rows of elements, then its order is 2×3. In the same way, when a matrix has an equal number of rows and columns, then the matrix is called the square matrix. In this article, you will learn the mathematical definition of a square matrix, properties of square matrix and examples in detail.

Learn: Matrices

Square Matrix Definition

A square matrix is a matrix that has an equal number of rows and columns. In mathematics, m × m matrix is called the square matrix of order m. If we multiply or add any two square matrices, the order of the resulting matrix remains the same.

Square Matrix Example

\(X=\left[\begin{array}{lll}2 & -7 & 7 \\ 2 & 5 & 6 \\ 5 & 4 & 3\end{array}\right]\)

In the above example, we can see, the number of rows and columns are three respectively. Since the order of the matrix is 3 × 3, hence X is a square matrix. We can also find the determinant of a 3×3 square matrix here.

Again, if we take another example, such as;

\(Y=\left[\begin{array}{lll}9 & 5 & 7 \\ 3 & 8 & 9\end{array}\right]\)

Here, the number of rows is two and the number of columns is 3. Since rows and columns of matrix Y are not equal, hence it is not a square matrix.

Square Matrix of Order 2

The square matrix of order 2 is the matrix with 2 rows and 2 columns. The general form of a 2×2 matrix or the square matrix of order 2 is given by:

\(A =\begin{bmatrix} a_{11} &a_{12} \\ a_{21}&a_{22} \end{bmatrix}\)

Square Matrix of Order 3

A square matrix of order 3 contains 3 rows and 3 columns, that means its order is 3×3. The general form of square matrix with order 3 is given as:

\(A =\begin{bmatrix} a_{11} &a_{12} & a_{13}\\ a_{21}&a_{22} & a_{23}\\ a_{31}&a_{32}&a_{33} \end{bmatrix}\)

Addition of Square Matrix

As we have already mentioned in the introduction part, that two square matrices can be added in a very simple way. Let us consider there is 3 by 3 matrix A and B whose values are given here:

\(\begin{array}{l}\left[\begin{array}{lll}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{21} & a_{22} & a_{23}\end{array}\right]+\left[\begin{array}{lll}b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \\ b_{21} & b_{22} & b_{13}\end{array}\right]=\left[\begin{array}{llll}a_{11}+b_{11} & a_{12}+b_{12} & a_{13}+b_{13} \\ a_{21}+b_{21} & a_{22}+b_{22} & a_{23}+b_{23} \\ a_{31}+b_{21} & a_{32}+b_{12} & a_{33}+b_{23}\end{array}\right] \\ For Example:\left[\begin{array}{lll}1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9\end{array}\right]+\left[\begin{array}{ccc}10 & 11 & 12 \\ 13 & 14 & 15 \\ 16 & 17 & 18\end{array}\right]=\left[\begin{array}{ccc}1+10 & 2+11 & 3+12 \\ 4+13 & 5+14 & 6+15 \\ 7+16 & 8+17 & 9+18\end{array}\right] \\ =\left[\begin{array}{ccc}11 & 13 & 15 \\ 17 & 19 & 21 \\ 23 & 25 & 27\end{array}\right]\end{array}\)

As we can see from the above example, the addition of square matrices is very important to perform. Each value in one matrix of a row is added to the other value of the same row and column of another matrix.

Multiplication of Square Matrix

Just like the addition method, the two square matrices are multiplied in the simple way. Let us consider two 2 by 2 square matrices to be multiplied together. Hence, the resultant matrix will be:

\(\begin{array}{l}\left[\begin{array}{lll}a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right]+\left[\begin{array}{lll}b_{11} & b_{12} \\ b_{21} & b_{22} \end{array}\right]=\left[\begin{array}{llll}a_{11}b_{11}+ a_{12}b_{12} & a_{11}b_{12}+ a_{12}b_{22} \\ a_{21}b_{11}+a_{22}b_{21} & a_{21}b_{12}+a_{22}b_{22} \end{array}\right] \end{array}\)

Note: The number of rows and columns should always be the same.

Square Matrix Determinant

The determinant of a matrix is the scalar value or a number estimated using a square matrix. The square matrix could be any number of rows and columns such as 2×2, 3×3, 4×4, or in the form of n × n, where the number of columns and rows are equal.

Check: Determinant of a Matrix

If S is the set of square matrices, R is the set of numbers (real or complex) and f : S → R is defined by f (A) = k, where A ∈ S and k ∈ R, then f (A) is called the determinant of A. The determinant of a square matrix A is denoted by “det A” or | A |.

For a 2 by 2 matrix, the determinant is given by:

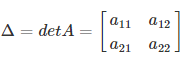
det A = a₁₁×a₂₂-a₁₂×a₂₁

Hence, we can find the determinant using this formula.

Square Matrix Properties

Some of the important properties of square matrices are listed below:

• The number of rows and columns is equal.
• The sum of all the diagonal elements of a square matrix is called the trace of a matrix.
• If all the diagonal elements of a square matrix are equal to 1, then it is called an identity matrix.
• For a square matrix, we can perform different operations such as inverse.
• The determinant value can be calculated only for the square matrix.
• The order of transpose of a square matrix is the same as the original matrix.