Square Root Finder
Square root finder helps you to find the square root of numbers which are squares of non-negative integers. Such as to find the square root of 4 you need to enter the (√a) value on ‘a’ and it will show you the value as 2 and (-2) but for the preference we choose 2. The symbol of the square root is ‘√’, which is called radical. If √a is the square root of a number a, then a is called here radicand.
We find square root of any gven number which is square of some positive integer. Suppose, we have to find the square root of 9. We know 9 = 3 x 3 or when 9 is the square of 3. Therefore the root of 9 will equal to 3. This is a very generic case, where the number inside the square root is a perfect square. But if we have to find the square root of imperfect squares, we have to use other methods. One of the method is long division method. But since it is a little complicated, we have come here to find the square root by some simple tricks. Before, we proceed let us see the tree diagram of finding root of a number.
Suppose we are looking to find the value of √64
Prime factorizing the number 64 we can divide the entire number by 2 such as:
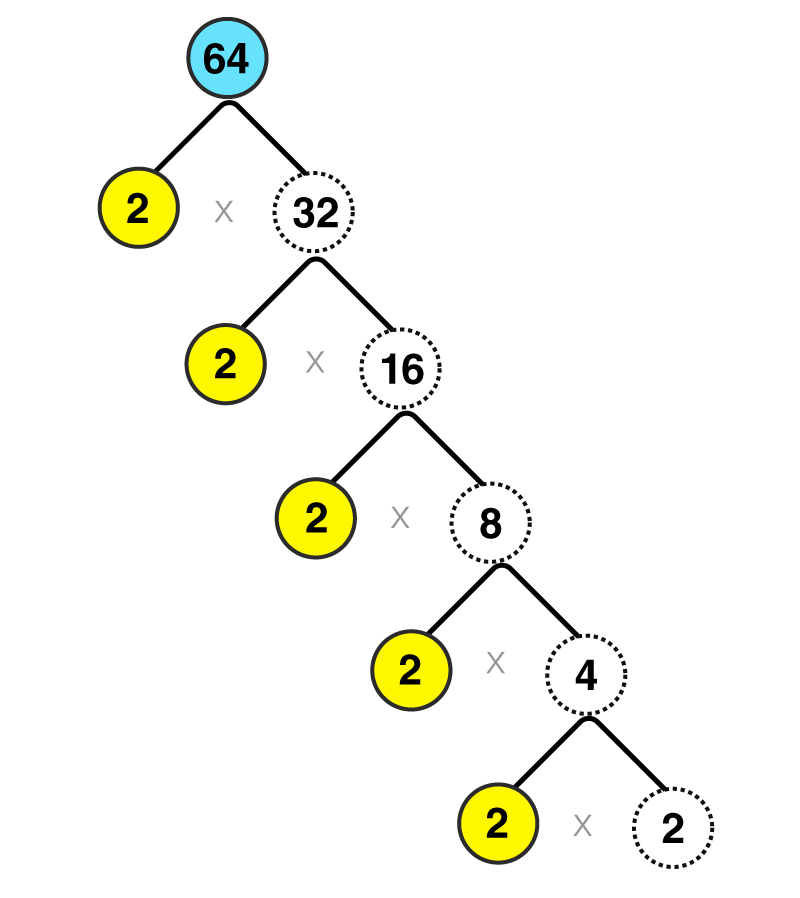
64= 2 x 32
32= 2 x 16
16= 2 x 8
8 = 2 x 4
4 = 2 x 2
So prime factorization of 64 is 2 x 2 x 2 x 2 x 2 x 2 which can be written as (2 x 2 x 2) x (2 x 2 x 2)= 8 x 8 =(8)2= 64
That is how you could find the square root of 64 which is 8.
By using the square root function, here we have found the square root of the first 10 numbers.
| √4 | 2 | Since 22 = 4 |
| √9 | 3 | Since 32 = 9 |
| √16 | 4 | Since 42 = 16 |
| √25 | 5 | Since 52 = 25 |
| √36 | 6 | Since 62 = 36 |
| √49 | 7 | Since 72 = 49 |
| √64 | 8 | Since 82 = 64 |
| √81 | 9 | Since 92 = 81 |
| √100 | 10 | Since 102 = 100 |
| √121 | 11 | Since 112 = 121 |
Also, read:
Finding Square Root of Imperfect Squares
Suppose a number whose square root has to be estimated is given to us. Let that number be n. Now, n here is an imperfect square. Follow the below steps:
- Find the two nearest perfect squares roots which are close to n
- Divide the given number by one of those numbers
- Take the average of the number produced and the root
- Check if we square this average, results in original number or not.
- If it doesn’t then repeat the above steps.
Example
Now let us see an example for it. Suppose we need to find the square root of 10. Then we have here;
The nearest perfect squares are 32 = 9 and 42 = 16, therefore, the root 10 lies between 3 and 4.
Now divide the number 10 by 3
10/3 = 3.33
Take the average of 3 and 3.33
(3+3.33)/2 = 3.1667
The square of 3.1667 is 10.02798889. The value is not near to 10. So repeat the steps.
Again divide 10 by 3.1667
10/3.1667 = 3.1579
Now take the average of 3.1667 and 3.1579
(3.1667+3.1579)/2 = 3.1623
Again square of 3.1623 is 10.0001, which is approximately equal to 10.
Hence, we can say √10 = 3.1623