Square Root of 20
The value of the square root of 20 is 4.472135955 and is denoted as √20 in radical form. This value we can easily get from the calculator. But, students should know how to simplify the root of any number without using a calculator. This is possible by using two methods: Prime factorisation and long division method. Both methods are very simple and are easy ways to find the square root.
|
Square root of 20, √20 = 4.4721 (in round figures) |
The square root of 20 is represented as √20, where √ is the radical sign and 20 is said to be radicand. In the simplest form, the √20 can be written as 2√5. Therefore, here we cannot say that √20 is a rational number since √5 is an irrational number.
Now, let us learn here to find the value of √20.
Simplification of Square Root of 20
The simple method to find the value of √20 is to factorise the number under the root, i.e. 20.
The prime factorisation of 20 gives:
20 = 2 x 2 x 5 = 22 x 5
Thus, here we can see, 20 is not a perfect square, because we cannot pair digit 5 after factoring 20. Only 22 can be taken out of the root.
Hence, if we take the roots on both sides, we get;
√20 = √(2 x 2 x 5)
Here, we just have only one pair of numbers, which is 2. Therefore, taking it outside the root, we get;
√20 = 2√5
From the square root table, we know the value of √5 = 2.236
Hence,
√20 = 2 x 2.236
√20 = 4.472
Using Long Division Method
We have learned to calculate the value of the square root of 20 using prime factorisation. But it is not a direct method to find the value because 20 is an imperfect square and we need to remember the √5 value to find the accurate value of √20.
By using long division method, we can use the accurate value of √20. Below is the solved step presented to evaluate √20.
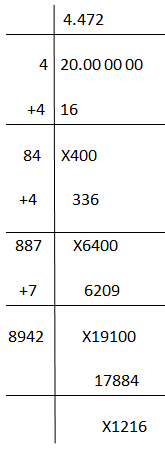
Find more square roots here: