Every one of us would have encountered multiple situations in life where we had to take a chance or risk. Depending on the situation, it can be predicted up to a certain extent if a particular event is going to take place or not. This chance of occurrence of a particular event is what we study in probability. In our everyday life, we are more accustomed to the word ‘chance’ as compared to the word ‘probability’. Since Mathematics is all about quantifying things, the theory of probability basically quantifies these chances of occurrence or non-occurrence of certain events. In this article, we are going to discuss what is probability and its two different types of approaches with examples.

What is Probability?

In Mathematics, the probability is a branch that deals with the likelihood of the occurrences of the given event. The probability value is expressed between the range of numbers from 0 to 1. The three basic rules connected with the probability are addition, multiplication, and complement rules.

Theoretical Probability Vs Experimental Probability

Probability theory can be studied using two different approaches:

• Theoretical Probability
• Experimental Probability

Theoretical Probability Definition

Theoretical probability is the theory behind probability. To find the probability of an event using theoretical probability, it is not required to conduct an experiment. Instead of that, we should know about the situation to find the probability of an event occurring. The theoretical probability is defined as the ratio of the number of favourable outcomes to the number of possible outcomes.

Probability of Event P(E) = No. of. Favourable outcomes/ No. of. Possible outcomes.

Experimental Probability Definition

The experimental probability also is known as an empirical probability, is an approach that relies upon actual experiments and adequate recordings of occurrence of certain events while the theoretical probability attempts to predict what will happen based upon the total number of outcomes possible. The experimental Probability is defined as the ratio of the number of times that event occurs to the total number of trials.

Probability of Event P(E) = No. of. times that event occurs/ Total number of trials

The basic difference between these two approaches is that in the experimental approach; the probability of an event is based on what has actually happened by conducting a series of actual experiments, while in theoretical approach; we attempt to predict what will occur without actually performing the experiments.

Theoretical probability Example

Question:

Find the probability of rolling a 5 on a fair die

Solution:

To find the probability of getting 5 while rolling a die, an experiment is not needed. We know that there are 6 possible outcomes when rolling a die. They are 1, 2, 3, 4, 5, 6.

Therefore, the probability  is,

Probability of Event P(E) = No. of. Favourable outcomes/ No. of. Possible outcomes.

P(E) = 1/6.

Hence, the probability of getting 5 while rolling a fair die is 1/6.

Comparing Experimental and Theoretical probability

Suppose in a cricket match tournament you are the captain of your team. Now, you are on the pitch and umpire tosses a fair coin. Can you predict the consequence or the outcome when the coin is still in the air? No, that is not possible. In this particular situation, tossing a coin in terms of probability is known as an experiment; this experiment is a random experiment since the result is unknown. Therefore, experiments which do not have a fixed result are known as random experiments. The consequence of such experiments is unknown. The result obtained after a random experiment has occurred is known as the outcome of that experiment. In this case, the possible outcomes are Head or Tail. Each outcome of an experiment or a collection of outcomes constitutes an event. If each outcome of an experiment has an equal chance of occurrence then these outcomes are equally likely. As in the example of tossing a fair coin, the chances of occurrence of heads and tails are equally likely. The entire possible set of outcomes of any experiment represents the sample space related to that experiment. The sample space related to any event is represented as S.

To determine the likelihood of random experiments they are repeated several times. An experiment is repeated a fixed number of times and each repetition is known as a trial.

The ratio of a number of favourable outcomes to the number of total outcomes is defined as the probability of occurrence of any event P(E) when the outcomes are equally likely.

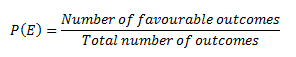
For any event the probability of its occurrence always lies between 0 and 1, i.e. 0 < P(E) <1. Also, if an event is sure to happen then its probability is 1 and if it is impossible to occur then its probability is 0. If P(E) is the probability of occurrence of any event and P(E)’ is the probability of non-occurrence of that event then;

P(E) + P(E)’ = 1

It has been observed that the experimental probability of an event approaches to its theoretical probability if the number of trials of an experiment is very large. But the question arises; what is the necessity to study theoretical probability when real-life experiments can be conducted? The answer is pretty simple since in a lot of cases, actually conducting many experiments is either not achievable or it’s too expensive.

Consider the experiment of tossing a coin or drawing a card from a deck of cards, this can be repeated a huge number of times to get a better result. But in situations, like to find the probability of failure of a satellite launch, experiments cannot be conducted multiple numbers of times because launching a satellite using rockets multiple numbers of times is neither feasible nor practical. In such cases, it becomes very crucial to make certain assumptions and based on those assumptions theoretical probability is calculated, which is very useful in such cases, especially in a lot of applications where we cannot perform the experiment.

To know more about experimental probability and theoretical probability please download BYJU’S The Learning App.