Trigonometry Angles
The angles by which trigonometric functions can be represented are called as trigonometry angles. The important angles of trigonometry are 0°, 30°, 45°, 60°, 90°. These are the standard angles of trigonometric ratios, such as sin, cos, tan, sec, cosec, and cot. Each of these angles has different values with different trig functions.
Table of Contents:
The two rays that have the same beginning point that forms the figure called an angle. The same beginning point is called the vertex and those two rays are called the sides of the angle which is also called as legs. Let us discuss in detail all the angles.
What are Trigonometry Angles?
Trigonometry angles are the angles given by the ratios of the trigonometric functions. Trigonometry deals with the study of the relationship between angles and the sides of a triangle. The angle value ranges from 0-360 degrees. The important angles in trigonometry are 0°, 30°, 45°, 60°, 90°, 180°, 270° and 360°. And the important six trigonometric ratios or functions are sine, cosine, tangent, cosecant, secant and cotangent.
Before discussing the trig angles, let us have a look at the definition of angle, and its related terminologies. Trigonometry is an important topic for Class 10, 11 and 12. Hence, it is required for students to learn the concept in a detailed manner to excel in the exam. Learn all the related trigonometric topics here with us at BYJU’S.
Radians and Degrees
The two common measurements used for determining angles are degree and radians. The most familiar unit of measurement of an angle is a degree. Consider, a circle is divided into 360 equal parts, where we can get the right angle with 900. Further, each degree is subdivided into 60 minutes and each minute is again subdivided into 60 seconds. The symbols used for degrees, minutes and seconds are °, ‘ and ” respectively. Minutes and seconds are also stated as arcminutes and arcseconds.
Beyond practical geometry in mathematics, angles are also used to measure in radians. The circle with the angle of 1 radian determines an arc with the length of the radius. Because the length of the full circle is 2πr. Alternatively, we can say that the circle contains 2π radians. The subdivision of radians is also written in decimal forms.
Because 2 π = 360°, the following conversion formulas has to be applied.
- r rad → [ 360.r/2π ]°
- g°→ [ 2π .g/360] rad
Trigonometry Table of all Angles (0 to 360)
Here there are some special angles provided with the trigonometric numbers. To simplify the way of calculation of the trigonometric numbers at various angles, reference angles are used which are derived from the primary trigonometric functions. We can derive values in degrees like 0°, 30°, 45°, 60°, 90°, 180°, 270° and 360°. The trigonometric table is given below, which defines all the values of trigonometric ratios.
| Angle (in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Angle (in Radians) | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 | 2π |
| Sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
| Cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| Tan | 0 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| Cot | ∞ | √3 | 1 | 1/√3 | 0 | ∞ | 1 | ∞ |
| Sec | 1 | 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 |
| Cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
Important Angles of Trigonometry
The special angles used in trigonometry are 0°, 30°, 45°, 60° and 90°. These are the common angles which are used while performing computations of trigonometric problems. Hence, it is suggested for students to memorise the values of trigonometric ratios (sine, cosine and tangent) for these angles, to do quick calculations.
Positive and Negative Angles
The angles could be positive or negative in nature. If the angle is formed in a counterclockwise direction from the start point in an x-y plane, then it is positive and if the angle is formed in a clockwise direction from the start point then it is a negative angle.
Angles More Than 360°
Once a complete cycle is done in an x-y plane, that means if we start the cycle from 0° and ends at 360°, a full circle is made. One full cycle also resembles a unit circle. After that, if we still keep going then the angles are greater than 360°. Now beyond 360° at each quadrant, you will get the angles, such as 450°, 540°, 630°, 720°, and so on. At 720° two cycles are completed and with respect to radians, it is measured as 4π. Similarly, the value of radians at each cycle is increased as n x 2π. So we can show this in a table as:
| Number of Cycle | Angle (n x 360°) | Radians (n x 2π) |
| 1 | 360° | 2π |
| 2 | 720° | 4π |
| 3 | 1080° | 6π |
| 4 | 1440° | 8π |
Trigonometry Angles Formulas
The formulas for trigonometry angles are based on the four quadrants of a unit circle. See the figure below to understand.
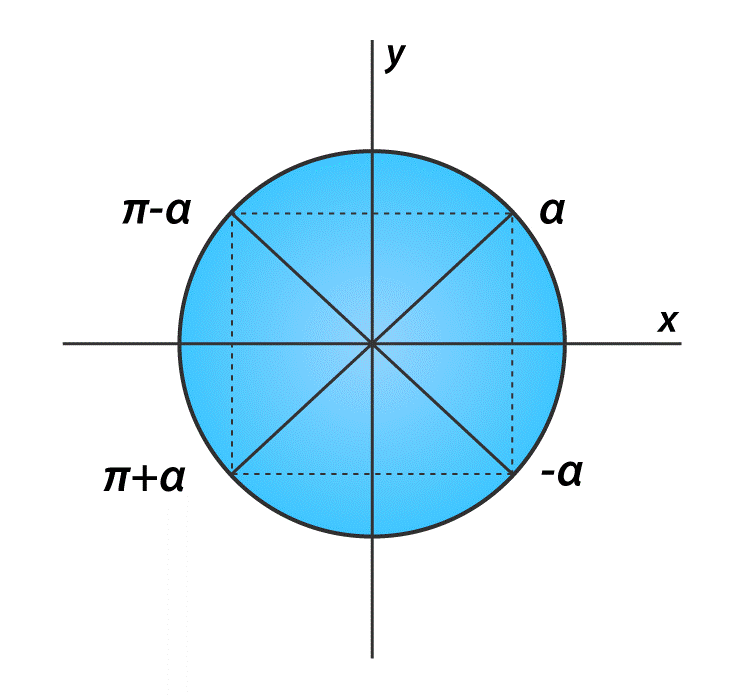
Supplementary angles ( = sum is π)
- Sin ( π – α ) = sin α
- Cos (π – α ) = – cos α
- Tan (π – α ) = – tan α
- Cot (π – α) = – cot α
Anti-supplementary Angles (= difference is π)
- Sin ( π + α ) = – sin α
- Cos (π + α ) = – cos α
- Tan (π + α ) = tan α
- Cot (π + α ) = cot α
Opposite Angles ( = sum is 2π)
- Sin ( 2π – α ) = – sin α
- Cos (2π – α ) = cos α
- Tan (2π – α ) = -tan α
- Cot (2π – α ) = – cot α
Complementary Angles (= sum is π/2)
- Sin ( π/2 – α ) = cos α
- Cos (π/2 – α ) = sin α
- Tan (π/2 – α ) = cot α
- Cot (π/2 – α ) = tan α
Also, see: Trigonometry Formulas
Examples
Question 1: Find the value of sin 60 – cos 30.
Solution:
The value of sin 60 = √3/2
Value of cos 30 = √3/2
Hence, sin 60 – cos 30 = √3/2 – √3/2 = 0
Question 2: Evaluate the value of 3sin 30 + tan 45
Solution:
Value of sin 30 = 1/2
Value of tan 45 = 1
By putting the values we get;
=3(1/2)+1
=3/2+1
=5/2
Question 3: If sin 3A = cos (A-26°), where 3A is an acute angle, find the value of A.
Solution:
Given that, sin 3A = cos (A-26°) ….(1)
Since, sin 3A = cos (90° – 3A), we can write (1) as:
cos(90°- 3A)= cos (A- 26°)
Since, 90°-3A = A – 26°
Therefore,
90° + 26° = 3A + A
4 A = 116°
A = 116° / 4 = 29°
Therefore, the value of A is 29°.
Question 4: If α = 60° and β = 30°, prove that sin (α – β) = sin α cos β – cos α sin β.
Solution:
L.H.S. = sin (α – β)
= sin (60° – 30°)
= sin 30°
= ½
R.H.S. = sin α cos β – cos α sin β
= sin 60° cos 30° – cos 60° sin 30°
= (√3/2)×(√3/2)−(1/2)×(1/2)
= ¾ – ¼
= 2/4
= ½
Hence, L.H.S. = R.H.S. (Proved)
Question 5: If α = 30°, verify that 3 sin α – 4 sin3 α = sin 3α.
Solution:
L.H.S = 3 sin α – 4 sin3 α
= 3 sin 30° – 4. sin3 30°
= 3 ∙ (1/2) – 4 ∙ (1/2)3
= 3/2 – 4 ∙ 1/8
= 3/2 – ½
= 1
R.H.S. = sin 3α
= sin 3 ∙ 30°
= sin 90°
= 1
Hence, L.H.S. = R.H.S. (Proved)
Related Links:
Keep visiting BYJU’S for more information on trigonometric ratios and its related articles, and also watch the videos to clarify the doubts.