A pair of sets which does not have any common element are called disjoint sets. For example, set A={2,3} and set B={4,5} are disjoint sets. But set C={3,4,5} and {3,6,7} are not disjoint as both the sets C and D are having 3 as a common element. Learn more about Disjoint Set here.

The Venn diagram of a disjoint set is given here:

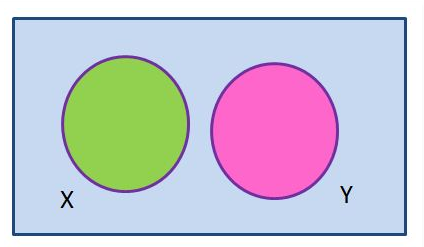
Another definition: When the intersection of two sets is a null or empty set, then they are called disjoint sets. Hence, if A and B are two disjoint sets, then;

A ∩ B = ϕ

Definition of disjoint sets can be extended further to a family of sets (A_i)_i i∈ I: the family is disjoint if A_i ⋂ A_j = Φ whenever i ≠ j. When coming to the notation for families, it can be defined as the notion of pairwise disjoint or mutually disjoint is sometimes defined in a subtly different manner, in that repeated identical members are allowed.

Pairwise Disjoint Sets

A group of sets is called pairwise disjoint if any two sets in the group are disjoint. It is also called mutually disjoint sets. Let A be the set of any group of sets and P and Q are two sets in set A

i.e. P, Q ∈ A. Then, A is called pairwise disjoint if and only if P ≠ Q. Therefore, P ∩ Q = ϕ

Related Links

Solved Problems

Q.1: Show that set A={2,5,6} and set B={4,7,8} are disjoint sets.

Solution: Given:

set A={2,5,6}

set B={4,7,8}

To prove: Set A and Set B are disjoint.

Proof: Two sets are disjoint if their intersection results to the null set.

Therefore,

A ∩ B = {2,5,6} ∩ {4,7,8}

As you can see, A and B do not have any common element.

So, A ∩ B = {}

Hence, proved A and B are disjoint.

Q.2 Are the set P={3,8,9} and set Q={9, 10,11}, disjoint sets? If no justify your answer.

Solution: set P={3,8,9}

set Q={9, 10,11}

P ∩ Q = {3,8,9} ∩ {9, 10,11}

= {9}

Since, the intersection of the two sets P and Q results to a common element {9}, therefore P and Q are not disjoint sets.

Q.3: State whether {a, e, i, o, u} and {a, b, c, d} are disjoint sets or not.

Solution: Suppose, A = {a, e, i, o, u} and

B = {a, b, c, d}

Now we have to find the intersection of the two sets, such as;

A ∩ B = {a, e, i, o, u} ∩ {a, b, c, d}

A ∩ B = {a}

Since the intersection of the two sets does not result in a null set, therefore, {a, e, i, o, u} and {a, b, c, d}are not disjoint sets.