Whole Numbers
The whole numbers are the part of the number system in which it includes all the positive integers from 0 to infinity. These numbers exist in the number line. Hence, they are all real numbers. We can say, all the whole numbers are real numbers, but not all the real numbers are whole numbers. Thus, we can define whole numbers as the set of natural numbers and 0. Integers are the set of whole numbers and negative of natural numbers. Hence, integers include both positive and negative numbers including 0. Real numbers are the set of all these types of numbers, i.e., natural numbers, whole numbers, integers and fractions.
The complete set of natural numbers along with ‘0’ are called whole numbers. The examples are: 0, 11, 25, 36, 999, 1200, etc.
Learn more about numbers here.
| Table of contents: |
Whole Numbers Definition
The whole numbers are the numbers without fractions and it is a collection of positive integers and zero. It is represented by the symbol “W” and the set of numbers are {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,……………}. Zero as a whole represents nothing or a null value.
|
These numbers are positive integers including zero and do not include fractional or decimal parts (3/4, 2.2 and 5.3 are not whole numbers). Addition, Subtraction, Multiplication and Division operations are possible on whole numbers.
Symbol
The symbol to represent whole numbers is the alphabet ‘W’ in capital letters.
W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…}
Thus, the whole numbers list includes 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ….
Facts:
|
If you still have doubt, What is a whole number in maths? A more comprehensive understanding of the whole numbers can be obtained from the following chart:
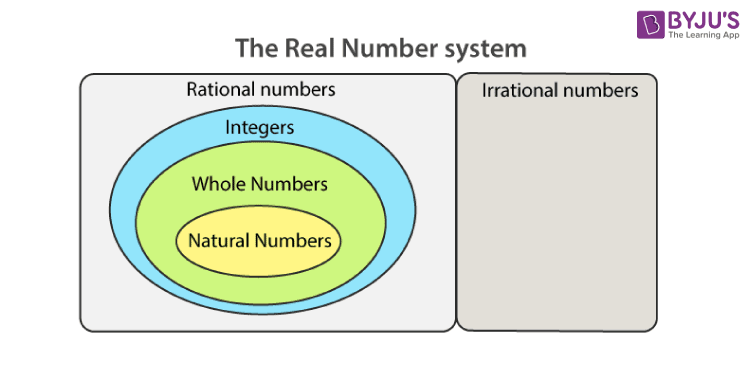
Whole Numbers Properties
The properties of whole numbers are based on arithmetic operations such as addition, subtraction, division and multiplication. Two whole numbers if added or multiplied will give a whole number itself. Subtraction of two whole numbers may not result in whole numbers, i.e. it can be an integer too. Also, division of two whole numbers results in getting a fraction in some cases. Now, let us see some more properties of whole numbers and their proofs with the help of examples here.
Closure Property
They can be closed under addition and multiplication, i.e., if x and y are two whole numbers then x. y or x + y is also a whole number.
Example:
5 and 8 are whole numbers.
5 + 8 = 13; a whole number
5 × 8 = 40; a whole number
Therefore, the whole numbers are closed under addition and multiplication.
Commutative Property of Addition and Multiplication
The sum and product of two whole numbers will be the same whatever the order they are added or multiplied in, i.e., if x and y are two whole numbers, then x + y = y + x and x . y = y . x
Example:
Consider two whole numbers 3 and 7.
3 + 7 = 10
7 + 3 = 10
Thus, 3 + 7 = 7 + 3 .
Also,
3 × 7 = 21
7 × 3 = 21
Thus, 3 × 7 = 7 × 3
Therefore, the whole numbers are commutative under addition and multiplication.
Additive identity
When a whole number is added to 0, its value remains unchanged, i.e., if x is a whole number then x + 0 = 0 + x = x
Example:
Consider two whole numbers 0 and 11.
0 + 11 = 0
11 + 0 = 11
Here, 0 + 11 = 11 + 0 = 11
Therefore, 0 is called the additive identity of whole numbers.
Multiplicative identity
When a whole number is multiplied by 1, its value remains unchanged, i.e., if x is a whole number then x.1 = x = 1.x
Example:
Consider two whole numbers 1 and 15.
1 × 15 = 15
15 × 1 = 15
Here, 1 × 15 = 15 = 15 × 1
Therefore, 1 is the multiplicative identity of whole numbers.
Associative Property
When whole numbers are being added or multiplied as a set, they can be grouped in any order, and the result will be the same, i.e. if x, y and z are whole numbers then x + (y + z) = (x + y) + z and x. (y.z)=(x.y).z
Example:
Consider three whole numbers 2, 3, and 4.
2 + (3 + 4) = 2 + 7 = 9
(2 + 3) + 4 = 5 + 4 = 9
Thus, 2 + (3 + 4) = (2 + 3) + 4
2 × (3 × 4) = 2 × 12 = 24
(2 × 3) × 4 = 6 × 4 = 24
Here, 2 × (3 × 4) = (2 × 3) × 4
Therefore, the whole numbers are associative under addition and multiplication.
Distributive Property
If x, y and z are three whole numbers, the distributive property of multiplication over addition is x. (y + z) = (x.y) + (x.z), similarly, the distributive property of multiplication over subtraction is x. (y – z) = (x.y) – (x.z)
Example:
Let us consider three whole numbers 9, 11 and 6.
9 × (11 + 6) = 9 × 17 = 153
(9 × 11) + (9 × 6) = 99 + 54 = 153
Here, 9 × (11 + 6) = (9 × 11) + (9 × 6)
Also,
9 × (11 – 6) = 9 × 5 = 45
(9 × 11) – (9 × 6) = 99 – 54 = 45
So, 9 × (11 – 6) = (9 × 11) – (9 × 6)
Hence, verified the distributive property of whole numbers.
Multiplication by zero
When a whole number is multiplied to 0, the result is always 0, i.e., x.0 = 0.x = 0
Example:
0 × 12 = 0
12 × 0 = 0
Here, 0 × 12 = 12 × 0 = 0
Thus, any whole number multiplied by 0, the result is always 0.
Division by zero
Division of a whole number by o is not defined, i.e., if x is a whole number then x/0 is not defined.
Also, check: Whole number calculator
Difference Between Whole Numbers and Natural Numbers
|
Difference Between Whole Numbers & Natural Numbers |
|
|---|---|
| Whole Numbers | Natural Numbers |
| Whole Numbers: {0, 1, 2, 3, 4, 5, 6,…..} | Natural Numbers: {1, 2, 3, 4, 5, 6,……} |
| Counting starts from 0 | Counting starts from 1 |
| All whole numbers are not natural numbers | All Natural numbers are whole numbers |
Below figure will help us to understand the difference between the whole number and natural numbers :
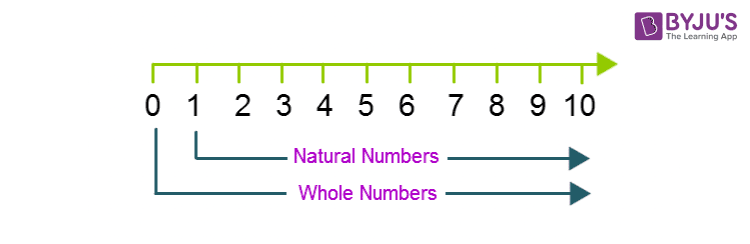
Can Whole Numbers be negative?
The whole number can’t be negative!
As per definition: {0, 1, 2, 3, 4, 5, 6, 7,……till positive infinity} are whole numbers. There is no place for negative numbers.
Is 0 a whole number?
Whole numbers are the set of all the natural numbers including zero. So yes, 0 (zero) is not only a whole number but the first whole number.
Solved Examples
Example 1: Are 100, 227, 198, 4321 whole numbers?
Solution: Yes. 100, 227, 198, 4321 are all whole numbers.
Example 2: Solve 10 × (5 + 10) using the distributive property.
Solution: Distributive property of multiplication over the addition of whole numbers is:
x × (y + z) = (x × y) + (x × z)
10 × (5 + 10) = (10 × 5) + (10 × 10)
= 50 + 100
= 150
Therefore, 10 × (5 + 10) = 150
However, we can show the several examples of whole numbers using the whole numbers properties.
To learn more concepts like natural numbers, real numbers in a more engaging way, register at BYJU’S. Also, watch interesting videos on various maths topics by downloading BYJU’S– The Learning App from Google Play Store or the app store.
Video lesson

Frequently Asked Questions on Whole Numbers
What are whole numbers?
The whole numbers are defined as the positive integers including zero. The whole number does not contain any decimal or fractional part. It means that it represents the entire thing without pieces. The set of whole numbers is mathematically represented as:
W = (0, 1, 2, 3, 4, 5,……}
Can whole numbers be negative?
No, the whole numbers cannot be negative. The whole numbers start from 0, 1, 2, 3, … and so on. All the natural numbers are considered as whole numbers, but all the whole numbers are not natural numbers. Thus, the negative numbers are not considered as whole numbers.
What are the properties of whole numbers?
The properties of whole numbers are:
Whole numbers are closed under addition and multiplication
The addition and multiplication of whole numbers is commutative
The addition and multiplication of whole numbers is associative
It obeys the distributive property of multiplication over addition
The additive identity of whole numbers is 0
The multiplicative identity of whole numbers is 1