Cross Section
Cross section means the representation of the intersection of an object by a plane along its axis. A cross-section is a shape that is yielded from a solid (eg. cone, cylinder, sphere) when cut by a plane.
For example, a cylinder-shaped object is cut by a plane parallel to its base; then the resultant cross-section will be a circle. So, there has been an intersection of the object. It is not necessary that the object has to be three-dimensional shape; instead, this concept is also applied for two-dimensional shapes.
Also, you will see some real-life examples of cross-sections such as a tree after it has been cut, which shows a ring shape. If we cut a cubical box by a plane parallel to its base, then we obtain a square.
| Table of contents: |
Cross-section Definition
In Geometry, the cross-section is defined as the shape obtained by the intersection of solid by a plane. The cross-section of three-dimensional shape is a two-dimensional geometric shape. In other words, the shape obtained by cutting a solid parallel to the base is known as a cross-section.
Cross-section Examples
The examples for cross-section for some shapes are:
- Any cross-section of the sphere is a circle
- The vertical cross-section of a cone is a triangle, and the horizontal cross-section is a circle
- The vertical cross-section of a cylinder is a rectangle, and the horizontal cross-section is a circle
Types of Cross Section
The cross-section is of two types, namely
- Horizontal cross-section
- Vertical cross-section
Horizontal or Parallel Cross Section
In parallel cross-section, a plane cuts the solid shape in the horizontal direction (i.e., parallel to the base) such that it creates the parallel cross-section
Vertical or Perpendicular Cross Section
In perpendicular cross-section, a plane cuts the solid shape in the vertical direction (i.e., perpendicular to the base) such that it creates a perpendicular cross-section
Cross-sections in Geometry
The cross sectional area of different solids is given here with examples. Let us figure out the cross-sections of cube, sphere, cone and cylinder here.
Cross-Sectional Area
When a plane cuts a solid object, an area is projected onto the plane. That plane is then perpendicular to the axis of symmetry. Its projection is known as the cross-sectional area.
Example: Find the cross-sectional area of a plane perpendicular to the base of a cube of volume equal to 27 cm3.
Solution: Since we know,
Volume of cube = Side3
Therefore,
Side3 = 27 [Given]
Side = 3 cm
Since, the cross-section of the cube will be a square therefore, the side of the square is 3cm.
Hence, cross-sectional area = a2 = 32 9 sq.cm.
Volume by Cross Section
Since the cross section of a solid is a two-dimensional shape, therefore, we cannot determine its volume.
Cross Sections of Cone
A cone is considered a pyramid with a circular cross-section. Depending upon the relationship between the plane and the slant surface, the cross-section or also called conic sections (for a cone) might be a circle, a parabola, an ellipse or a hyperbola.
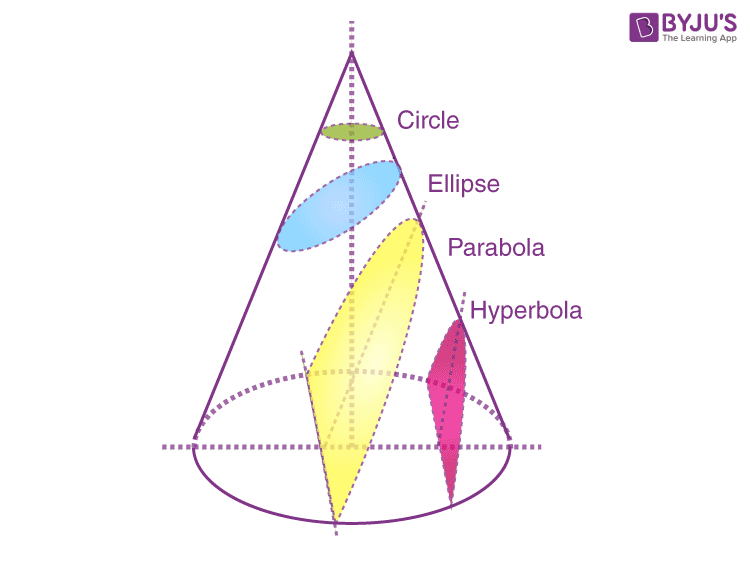
From the above figure, we can see the different cross sections of cone, when a plane cuts the cone at a different angle.
Also, see: Conic Sections Class 11
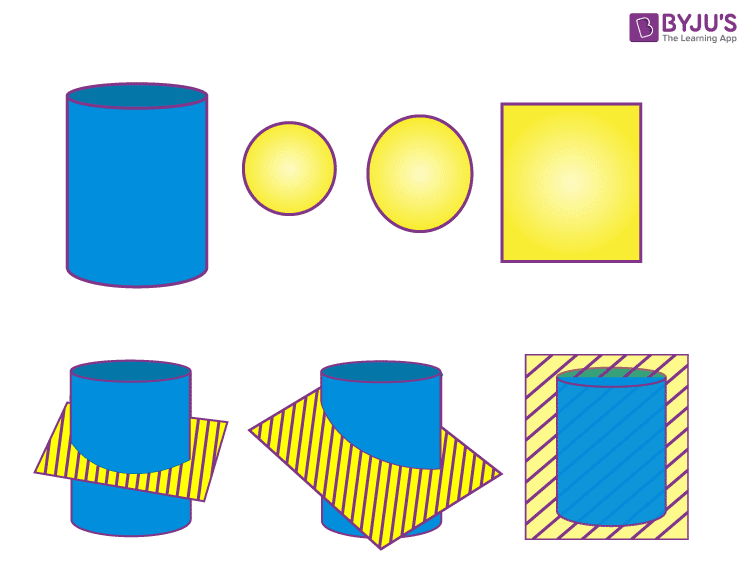
Cross Sections of cylinder
Depending on how it has been cut, the cross-section of a cylinder may be either circle, rectangle, or oval. If the cylinder has a horizontal cross-section, then the shape obtained is a circle. If the plane cuts the cylinder perpendicular to the base, then the shape obtained is a rectangle. The oval shape is obtained when the plane cuts the cylinder parallel to the base with slight variation in its angle
Cross Sections of Sphere
We know that of all the shapes, a sphere has the smallest surface area for its volume. The intersection of a plane figure with a sphere is a circle. All cross-sections of a sphere are circles.

In the above figure, we can see, if a plane cuts the sphere at different angles, the cross-sections we get are circles only.
Articles on Solids
Solved Problem
Problem:
Determine the cross-section area of the given cylinder whose height is 25 cm and radius is 4 cm.
Solution:
Given:
Radius = 4 cm
Height = 25 cm
We know that when the plane cuts the cylinder parallel to the base, then the cross-section obtained is a circle.
Therefore, the area of a circle, A = πr2 square units.
Take π = 3.14
Substitute the values,
A = 3.14 (4)2 cm2
A = 3.14 (16) cm2
A = 50.24 cm2
Thus, the cross section area of the cylinder is 50.24 cm2