Area of an Octagon
Area of an octagon is the region covered by an octagon in a two-dimensional plane. An octagon is a two-dimensional geometrical plane figure. In Geometry, we have studied different types of polygon shapes such as triangle, square, pentagon, hexagon, rectangle, etc. Like other shapes, the octagon is also a polygon.
Octagon has 8 sides and 8 angles. It means the number of vertices and edges are 8. All the sides of the octagon joined with each other end-to-end to form a shape. These sides are in a straight line segment. They are not curved or disjoint with each other.

Area of an Octagon Formula
The area of an octagon is defined as the total space occupied inside the boundary of an octagon. The measurement unit for the area is square units.
If a polygon is with eight equal sides and eight equal angles, then the polygon is a regular octagon. Otherwise, the polygon is known as an irregular polygon.
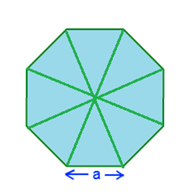
In the above figure, you can see the figure of a regular octagon, which is divided into eight equivalent triangles. The distance of each vertex from the centre is equal. Here, ‘a’ shows the length of the sides.
The area of an octagon formula is given as,
Area of a regular octagon, A = 2a2 (1+√ 2 ) Square units.
Where “a” is the length of the octagon sides.
It is not possible to find the area of an irregular octagon using this formula. So, to find its area, it is divided into other regular polygons. Then, the areas of all polygons should be added to get its area.
Area of an Octagon Examples
Question1: Find the area of regular octagon whose side is 5cm.
Solution:
Given:
Side, a = 5cm
We know that,
Area of a regular octagon, A = 2a2 (1+√ 2 ) Square units
A = 2(5)2 (1+√ 2 ) cm2
A = 2(25) (1+√ 2 ) cm2
A = 50 (1+√ 2 ) cm2
A = 50(1+1.414) cm2
A = 50(2.414) cm2
A = 120.7 cm2
Therefore, the area of a regular octagon is 120.7 cm2.
| Related Links | |
| Area of Polygon | Area of Quadrilateral |
| Area of Pentagon | Area of Hexagon |
Area of Irregular Octagon
Finding the area of a regular octagon is an easy task because you have been provided by a symmetric figure. A regular octagon has all its sides equal in length. But in the case of the irregular octagon, the sides have different dimensions and each angle could be different. Therefore, we have alternative methods to find the area. Hence, here we are providing some important steps to find the area of an irregular octagon.
- Break the given octagon into triangles.
- Find the area of the individual triangle
- Add all the areas to get the result.
Let us understand the above steps with the help of an example.
Question 2:
Find the area of an irregular octagon given below:
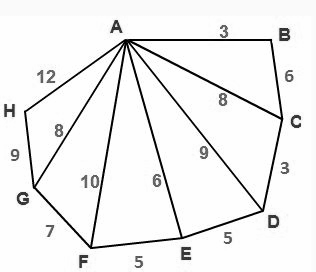
Solution:
The given figure is an irregular octagon.
Therefore, the area of an irregular octagon ABCDEFGH is given below:
Area of ABCDEFGH = Area of ABC + Area of ACD + Area of ADE +Area of ADE + Area of AFG + Area of AGH
Finding the area of ABC:
Using Heron’s Formula:
S = (3+6+8)/2
S = 8.5
Therefore, the area of ABC = \(\sqrt{S(S-a)(S-b)(S-c)}\) \(A =\sqrt{8.5(8.5-3)(8.5-6)(8.5-8)}=7.64\)
Therefore, the area of ABC = 7.64
Similarly, we can find the area of other triangles using Heron’s formula,
Area of ACD = 11.83
Area of ADE = 14.14
Area of ADE = 11. 39
Area of AFG = 27.81
Area of AGH = 35.99
Now, add all the areas of the triangle
Area of ABCDEFGH = 7.64 + 11.83 + 14.14 + 11. 39 + 27.81 + 35.99 = 108.83
Hence, the area of an irregular octagon is 108.83 square units
Visit BYJU’S – The Learning App to learn more Maths-related concepts and download the app to watch interesting videos.