A Key To The Laws Of Exponents
Can you read 10,000,000,000,000,000,000,000? This massive natural number is not easy to read, recognize and evaluate. Exponents make it easy to read, recognize and evaluate very large numbers. Exponents are also called powers or indices. What is meant by exponents? What are the laws of exponents? How to apply the laws of exponents to simplify expressions? Let us take an overview of the laws of exponents.
Learn: Exponent
Rules of Exponents With Examples
Exponents are defined as a number that tells how many times we have to multiply the base number. It is written above the right side of the base number.
1. 52 = “5 raised to the power of 2” or “5 squared.”
2. 53 = “5 raised to the power of 3” or “10 cubed.”
Example 1 :10,000 = 10 x 10 x 10 x 10 = 104
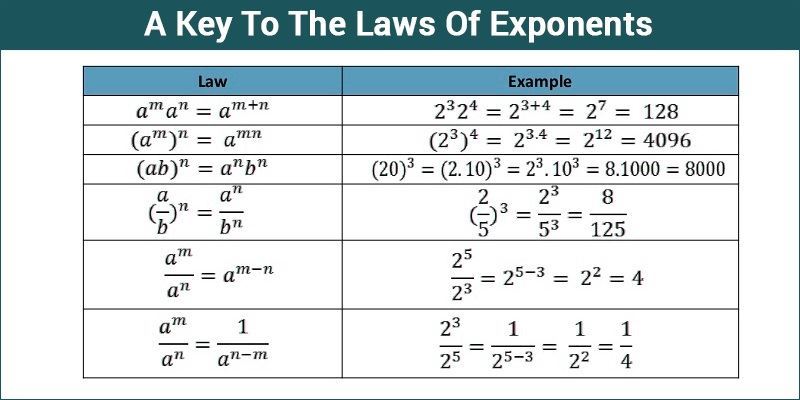
The laws of exponents state the following rules to simplify the expressions. Some of them are as follows:
Rule 1: When the numbers having the same base are multiplied, add the exponents.
ap × aq = a(p+q)
a = base : p,q = exponents
Example 1: Let us calculate,
32×34
Solution:
32 × 34 =3{(2+4)} = 36
In the above example, the base numbers are the same. (i.e.,) 32 and 34. The sum of the powers is 6.
Rule 2: When the numbers having the same base are divided, subtract the exponents.
ap ÷ aq = a{(p-q)} i.e. a = base: p,q = exponents
Example 2: 34 ÷ 32 =?
Solution:
34 ÷ 32 = 3{(4-2)} = 32
In the above example, the bases are the same. (i.e., 34 and 32).
Rule 3: Multiply the powers when the numbers are raised by another number.
(ap)q = a{(pxq)} =a{(pq)}
Example 3 : (23)2 =?
Solution: (23)2 = 2{(3×2)} = 26
Example problems
Example 1:
Multiplying powers with the same base
32 × 33 =?
Solution:
In the above example, as per rule 1, add the powers when the numbers are multiplied.
So,
32 × 33 = 3{(2+3)} = 35
Example 2:
Dividing powers with the same base
45 ÷ 42
Solution:
In the above example, as per rule 2, subtract the powers when the numbers are divided.
So,
45 ÷ 42 = 4{(5-2)} = 43
Example 3:
What is the value of 2 power 9 and 2 power 7?
Solution:
2 power 9 can be represented as 29.
The value of 2 power 9 = 29 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 512
The value of 2 power 7 = 27 = 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128
Practice Problems
- Find the value of (43)2.
- What is the value of 6-2. 65?
- Evaluate: (0.5)2
- Find the value of the product of 2 power 7 and 2 power 9.
Thus, we have seen this basic introduction and examples of the laws of exponents. For a complete understanding of the topic, please visit our site or download the BYJU’S – The Learning App.