commutative law, in mathematics, either of two laws relating to number operations of addition and multiplication, stated symbolically: a + b = b + a and ab = ba. From these laws it follows that any finite sum or product is unaltered by reordering its terms or factors. While commutativity holds for many systems, such as the real or complex numbers, there are other systems, such as the system of n × n matrices or the system of quaternions, in which commutativity of multiplication is invalid. Scalar multiplication of two vectors (to give the so-called dot product) is commutative (i.e., a·b = b·a), but vector multiplication (to give the cross product) is not (i.e., a × b = −b × a). The commutative law does not necessarily hold for multiplication of conditionally convergent series. See also associative law; distributive law.

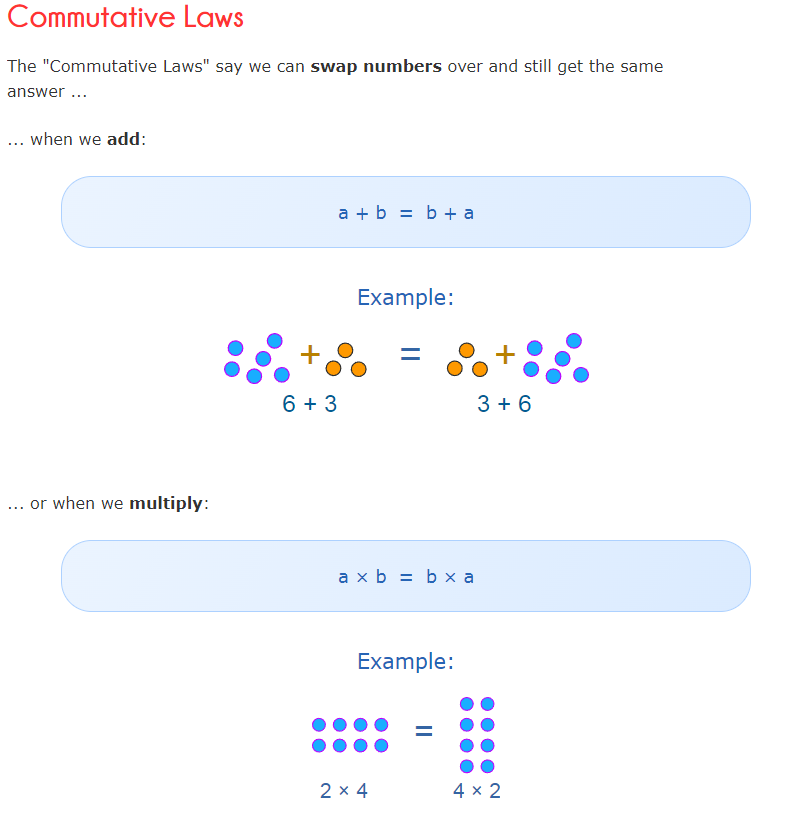
The Commutative Law

( "change" the order of the numbers or letters)

Over the years, people have found that when we add or multiply, the order of the numbers will

not affect the outcome.

5 + 4 is 9 and 4 + 5 is 9. The 5 and the 4 can be switched in addition.

9(2) is 18 and 2(9) is 18. The 9 and the 2 can be switched in multiplication.

"Switching" or "changing" the order of numbers is called "commuting".

People "commute" from home to work everyday. You travel from where you live to where you

work, and at the end of the day turn around to return to where you live.

When we change the order of the numbers, we have applied the "Commutative Law".

In an addition problem, it is referred to as the "Commutative Law of Addition".

In multiplication, it is the "Commutative Law of Multiplication."

The Commutative Law does not work for either subtraction or division.

The order of the numbers will affect the outcome.

When you write 100 - 25, it is very different from 25 - 100.

The first case could be likened to writing a $25 check when you have $100 in the bank.

The other case, 25 - 100, would be an example of writing a $100 check when you have $25 in

the bank. Oops.....

One must be cautious with subtraction. If we look at the operation of subtraction as "adding the

opposite" then there may be a way to "commute" the numbers, but in terms of addition and not

subtraction. 

In Mathematics, commutative law is applicable only for addition and multiplication operations. But, it is not applied to other two arithmetic operations, such as subtraction and division. As per commutative law or commutative property, if a and b are any two integers, then the addition and multiplication of a and b result in the same answer even if we change the position of a and b. Symbolically it may be represented as:

a+b=b+a

a×b=b×a

For example, if 2 and 5 are the two numbers, then;

2 + 5 = 5 + 2 = 7

2 × 5 = 5 × 2 = 10

Definition

The definition of commutative law states that when we add or multiply two numbers then the resultant value remains the same, even if we change the position of the two numbers. Or we can say, the order in which we add or multiply any two real numbers does not change the result.

Hence, if A and B are two real numbers, then, as per this law;

Note: Commutative law does not work for subtraction and division

Proof

It is easy to prove the commutative law for addition and multiplication. Let prove with examples.

Commutative Law of Addition

The commutative law of addition states that if two numbers are added, then the result is equal to the addition of their interchanged position.

A+B = B+A

Examples:

• 1+2 = 2+1 = 3

• 4+5 = 5+4 = 9

• -3+6 = 6+(-3) = 6-3 = 3

This law is not applicable for subtraction because if the first number is negative and if we change the position, then the sign of the first number will get changed to positive, such that;

(-A)-B = -A – B ……(1)

After changing the position of the first and second number, we get;

B – (-A) = B + A ….(2)

Hence, from equation 1 and 2, we can see that;

(-A)-B ≠ B-(-A)

For example: (-9)-2 = -9-2 = -11

& 2-(-9) = 2+9 = 11

Hence, -11 ≠ 11.

Commutative Law of Multiplication

As per this law, the result of the multiplication of two numbers stays the same, even if the positions of the numbers are interchanged.

Hence, A.B = B.A

Examples:

• 1×2 = 2×1 = 2

• 4×5 = 5×4 = 20

• -3×6 = 6×(-3) = -18

Commutative Law in Percentages

While finding the percentages, if we interchange or swap the order of the values, then the answer does not change. Mathematically we can say;

A% of B = B% of A

Example:

10% of 50 = 50% of 10

Since, 

10% of 50 = (10/100) x 50 = 5

50% of 10 = (50/100) x 10 = 5

Thus, the answer remains the same.

Associative and Distributive Laws

Apart from commutative law, there are other two major laws, which are commonly used in Maths, they are:

• Associative law

• Distributive law

Associative Law: As per this law, if A, B and C are three real numbers, then;

• A+(B+C) = (A+B)+C

• A.(B.C) = (A.B).C

Just like commutative rule, this law is also applicable to addition and multiplication.

For example: If 2,3 and 5 are three numbers then;

2+(3+5) = (2+3)+5

⇒2+8 = 5 + 5

⇒10 = 10

&

2.(3.5) = (2.3).5

⇒ 2.(15) = (6).5

⇒ 30 = 30

Hence, proved.

Distributive Law: This law is completely different from commutative and associative law. According to this law, if A, B and C are three real numbers, then;

A.(B+C) = A.B + A.C

For example: If 2,3 and 5 are three numbers then;

2.(3+5) = 2.3+2.5

2.(8) = 6+10

16 = 16

Commutative Law of Sets

Sets are the collection of elements or objects. In sets, we have learned about different types of operations performed on them such as intersection of sets, union of sets, difference of sets, etc.

According to the Commutative law for Union of sets and the Commutative law for Intersection of sets, the order of the sets in which the operations are done, does not change the result.

So, if A and B are two different sets, then, as per commutative law;

A ∪ B = B ∪ A  [Union of sets]

A ∩  B = B ∩ A   [Intersection of sets]

For example, if A = {1, 2, 3} and B = {3, 4, 5, 6}, then;

A Union B = A ∪ B = {1, 2, 3, 4, 5, 6}  …….. (i)

B Union A = B ∪ A = {1, 2, 3, 4, 5, 6}   ……… (ii)

From (i) and (ii), we get;

A ∪ B = B ∪ A

Now, 

A intersection B = A ∩ B = {3}   ……..(iii)

B intersection A = B ∩ A = {3}   ……..(iv)

From (iii) and (iv), we get;

A ∩ B = B ∩ A

Hence, proved commutative law for union and intersection of two sets.

Frequently Asked Questions – FAQs