Altitude Of A Triangle

Trigonometry

Trigonometry Logo

Altitude Of A Triangle

Home → Altitude Of A Triangle

The altitude of a triangle is the perpendicular line segment drawn from the vertex to the opposite side of the triangle. It may lie inside or outside the triangle, based on the types of triangles. The altitude of a triangle basically defines the height, when we have to measure the area of a triangle, with respect to the base. 

Table of Contents:

What is Altitude Of A Triangle?

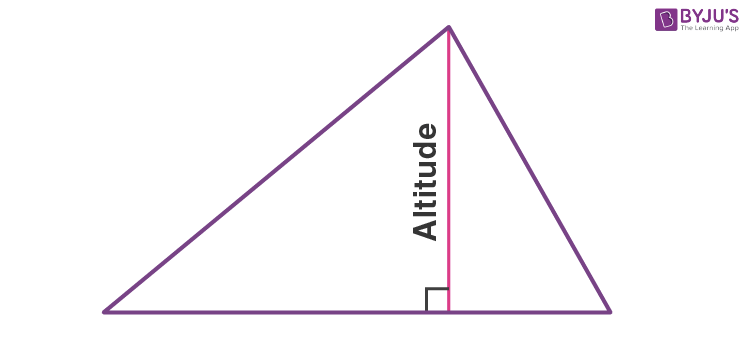
The altitude of a triangle is the perpendicular drawn from the vertex of the triangle to the opposite side. Also, known as the height of the triangle, the altitude makes a right-angle triangle with the base. Below is an image that shows a triangle’s altitude.


What is the Use of Altitude of a Triangle?

The main application use of altitude is that it is used for area calculation of the triangle, i.e. area of a triangle is (½ base × height). Now, using the area of a triangle and its height, the base can be easily calculated as Base = [(2 × Area)/Height]

Properties of Altitude of a Triangle

The different properties of altitude of a triangle are listed below:

  • There are a maximum of three altitudes for a triangle
  • The altitude of a triangle is perpendicular to the opposite side. Thus, it forms 90 degrees angle with the opposite side.
  • Depending on the type of triangle, the altitude can lie inside or outside the triangle
  • The point of intersection of three altitudes is called the orthocenter of the triangle

Altitudes of Different Triangles

About altitude, different triangles have different types of altitude. Below is an overview of different types of altitudes in different triangles.

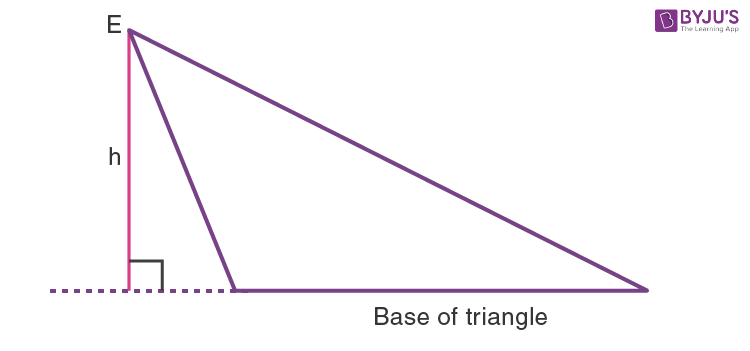
For an obtuse-angled triangle, the altitude is outside the triangle. For such triangles, the base is extended, and then a perpendicular is drawn from the opposite vertex to the base. For an obtuse triangle, the altitude is shown in the triangle below.

Altitude of an Obtuse Triangle


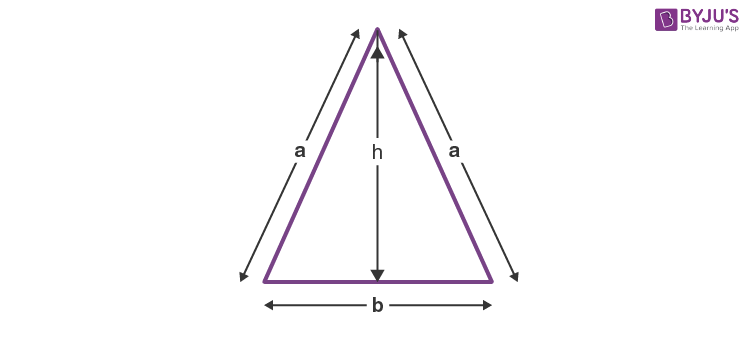
Altitude of an Equilateral Triangle

The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. The image below shows an equilateral triangle ABC where “BD” is the height (h), AB = BC = AC, ∠ABD = ∠CBD, and AD = CD.

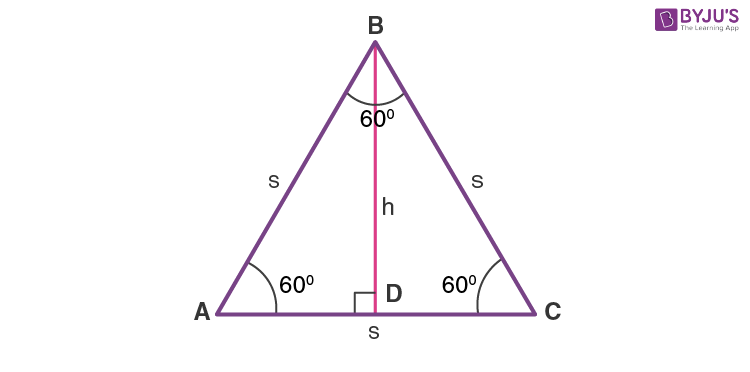
For an equilateral triangle, all angles are equal to 60°.

In triangle ADB,

sin 60° = h/AB

We know, AB = BC = AC = s (since all sides are equal)

∴ sin 60° = h/s

√3/2 = h/s

h = (√3/2)s

Therefore, the Altitude (Height) of an equilateral triangle = h = √(3⁄2) × s

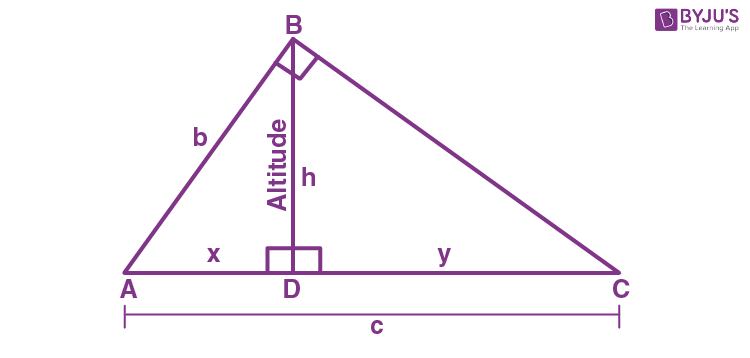
Altitude of a Right Triangle

The altitude of a right-angled triangle divides the existing triangle into two similar triangles. According to the right triangle altitude theorem, the altitude on the hypotenuse is equal to the geometric mean of line segments formed by altitude on the hypotenuse.

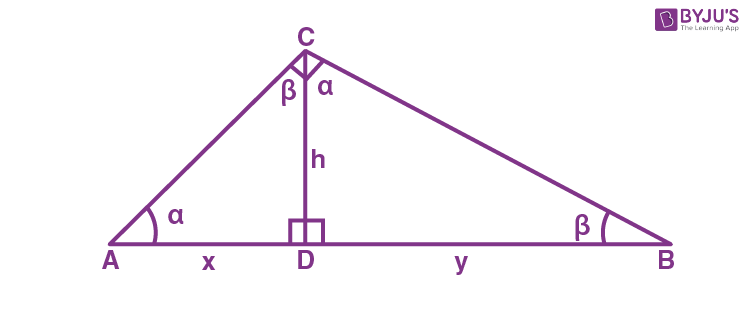
For a right triangle, when a perpendicular is drawn from the vertex to the hypotenuse, two similar right triangles are formed. This is called the right triangle altitude theorem.

In the above figure, 

△ADB ∼ △BDC

Thus,

AD/BD = BD/DC

BD2 = AD.DC

h2 = x.y

h = √xy

Hence, is the altitude of a right triangle.

Altitude of an Isosceles Triangle

The isosceles triangle altitude bisects the angle of the vertex and bisects the base. It should be noted that an isosceles triangle is a triangle with two congruent sides and so, the altitude bisects the base and vertex.


Altitudes of a Triangles Formulas

Triangle Type Altitude Formula
Equilateral Triangle h = (½) × √3 × s
Isosceles Triangle h =√(a2−b2⁄2)
Right Triangle h =√(xy)

Difference Between Median and Altitude of a Triangle

Median of triangle Altitude of triangle
Median is a line segment drawn from the vertex to the middle of the opposite side of a triangle. Altitude is drawn from the vertex and is perpendicular to the opposite side of the triangle
It bisects the opposite side It may or may not bisect the opposite side, based on the type of triangle
It lies inside the triangle always It may or may not lie inside the triangle, depending on the type of triangle
It divides the triangle into two equal parts It does not divide the triangle into two equal parts
The intersection point of the three medians is called the centroid of the triangle The intersection point of three altitudes is called the orthocenter of the triangle

Solved Examples

Q.1: What is the altitude of an equilateral triangle, if its side length is equal to 4 cm?

Solution: Given, the side length of an equilateral triangle is 4 cm.

The altitude of an equilateral triangle, h = s√3/2

= 4√3/2

= 2√3 cm

Q.2: If sides of a triangle are a = 3, b = 6, and c = 7, then what is the altitude of the triangle?

Solution: Since all the sides of the given triangle are unequal in length, thus it is a scalene triangle. 

Using the formula for altitude of scalene triangle, we have;

h = [2√(s(s−a).(s−b).(s−c))]/b

s = (a+b+c)/2 = (3+6+7)/2 = 16/2 = 8

h = [2√(8(8-3)(8-6)(8-7))]/2

h = [2√(8.5.2.1)]/2

h = 4√5

Practice Questions

  1. What is the height of an isosceles triangle, if the length of equal sides is 8 cm and the unequal side is 6 cm?
  2. Three sides of a given triangle are 8 units, 11 units, and 13 units. Find the length of altitude of the triangle.
  3. Find the height of an equilateral triangle whose side measures 10 cm.

Related Articles


Frequently Asked Questions – FAQs

What is an altitude of a triangle?

An altitude of a triangle is the perpendicular distance drawn from the vertex to the opposite side of the triangle.

What is the formula for an altitude of a triangle?

The formula for an altitude of a triangle varies for different triangles.
For scalene triangle, the altitude is [2√(s(s−a).(s−b).(s−c))]/b
For an equilateral triangle, the altitude is a√3/2
For an isosceles triangle, the altitude is √(a2 – b2/4)
For the right triangle, the altitude is √xy

Where does the altitude of an acute triangle lie?

The altitude of an acute triangle lies inside the triangle.

What is the property of the altitude of a triangle?

The altitude of a triangle lies inside or outside the triangle. It is at 90 degrees angle to the opposite side. The point of intersection of three altitudes is called the orthocenter of the triangle.

Is the altitude of an obtuse triangle inside the triangle?

No, the altitude of the obtuse triangle lies outside the triangle.

Keep visiting BYJU’S to learn various Maths topics in an interesting and effective way. Also, register now and download BYJU’S – The Learning App to get engaging video lessons and personalised learning journeys.