A quadrilateral whose two pairs of sides are parallel to each and the four angles at the vertices are not equal to the right angle, and then the quadrilateral is called a parallelogram. Also, the opposite sides are equal in length.

Here,

AD = BC (opposite sides)

AB = CD (opposite sides)

Sum of all the four angles = 360 degrees

Learn more about the parallelogram here.

The important properties of angles of a parallelogram are:

• If one angle of a parallelogram is a right angle, then all the angles are right angles
• Opposite angles of a parallelogram are equal (or congruent)
• Consecutive angles are supplementary angles to each other (that means they add up to 180 degrees)

Opposite Angles of a Parallelogram

In the above parallelogram, A, C and B, D are a pair of opposite angles.

Therefore, ∠A = ∠C and ∠B = ∠D

Also, we have different theorems based on the angles of a parallelogram. They are explained below along with proofs.

Opposite Angles of a Parallelogram are equal

Theorem: Prove that the opposite angles of a parallelogram are equal.

Given: Parallelogram ABCD.

To prove: ∠B = ∠D and ∠A =∠C

Proof:

In the parallelogram ABCD,

AB || CD and AD || BC

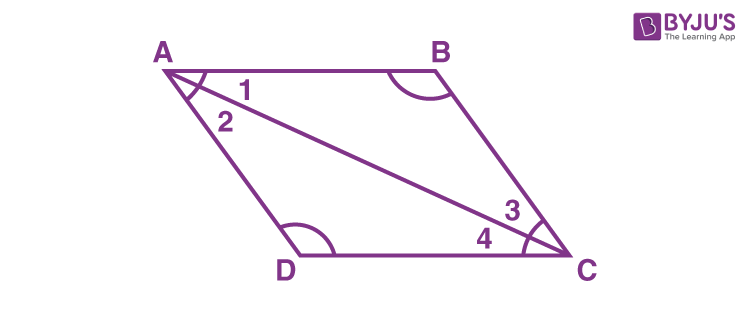
Consider triangle ABC and triangle ADC,

AC = AC (common side)

We know that alternate interior angles are equal.

∠1 = ∠4

∠2 = ∠3

By ASA congruence criterion, two triangles are congruent to each other.

Therefore, ∠B = ∠D and ∠A =∠C

Hence, it is proved that the opposite angles of a parallelogram are equal.

Consecutive Angles of a Parallelogram

Theorem: Prove that any consecutive angles of a parallelogram are supplementary.

Given: Parallelogram ABCD.

To prove: ∠A + ∠B = 180 degrees, ∠C + ∠D = 180 degrees

Proof:

AB ∥ CD and AD is transversal.

We know that interior angles on the same side of a transversal are supplementary.

Therefore, ∠A + ∠D = 180°

Similarly, ∠B + ∠C = 180°, ∠C + ∠D = 180° and ∠A + ∠B = 180°.

Therefore, the sum of any two adjacent angles of a parallelogram is equal to 180°.

Hence, it is proved that any two adjacent or consecutive angles of a parallelogram are supplementary.

If one angle is a right angle, then all four angles are right angles:

From the above theorem, it can be decided that if one angle of a parallelogram is a right angle (that is equal to 90 degrees), then all four angles are right angles. Hence, it will become a rectangle.

Since the adjacent sides are supplementary.

For example, ∠A, ∠B are adjacent angles and ∠A = 90°, then:

∠A + ∠B = 180°

90° + ∠B = 180°

∠B = 180° – 90°

∠B = 90°

Similarly, ∠C = ∠D = 90°

Solved Examples

Example 1:

In the adjoining figure, ∠D = 85° and ∠B = (x + 25)°, find the value of x.

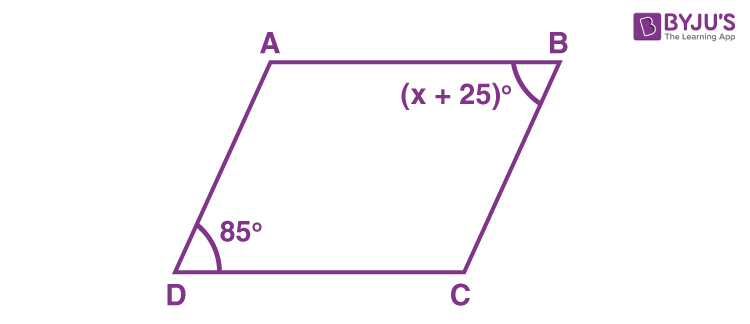
Solution:

Given,

∠D = 85° and ∠B = (x + 25)°

We know that opposite angles of a parallelogram are congruent or equal.

Therefore,

(x + 25)° = 85°

x = 85° – 25°

x = 60°

Hence, the value of x is 60.

Example 2: Observe the below figure.

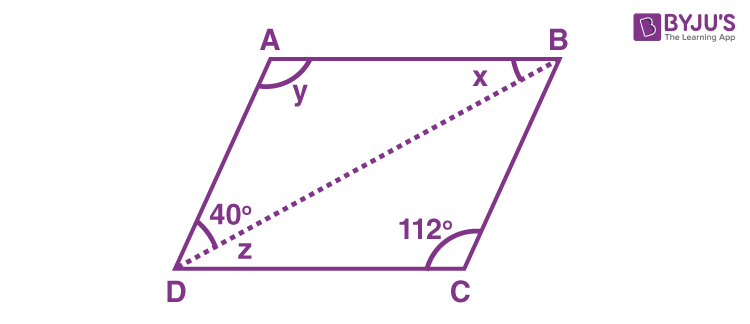
Find the values of x, y and z.

Solution:

From the given figure,

y = 112° {since the opposite angles of a parallelogram are equal)

z + 40° + 112° = 180° {the sum of consecutive angles is equal to 180°}

z = 180° – 112° – 40° = 28°

Also, x = 28° {x and x are alternate angles)

Therefore, x = 28°, y = 112° and z = 28°.

Example 3: 

Two adjacent angles of a parallelogram are in the ratio 4 : 5. Find their measures. 

Solution:
Given,

The ratio of two adjacent angles of a parallelogram  = 4 : 5

Let 4x and 5x the angles. 

Then, 4x + 5x = 180° {the sum of two adjacent angles of a parallelogram is supplementary}

9x = 180° 

x = 20° 

Therefore, the angles are 4 × 20° = 80° and 5 × 20° = 100°.

Practice Problems

1. Two adjacent angles of a parallelogram are in the ratio 5 : 1. Find all the angles of the parallelogram.
2. The opposite angles of a parallelogram are (3x – 4)° and (2x – 1)°. Find the measures of all angles of the parallelogram.
3. If one of the interior angles of a parallelogram is 100°, then find the measure of all the remaining angles.