Let us say that a line is inclined on a plane. A normal to the plane is drawn from the point where the line touches the plane. This normal forms an angle with the line. In analytic geometry, the angle between the line and the plane is equivalent to the complement of the angle between the line and the normal. In this section, we will discuss this concept in detail.

Angle between a Line and a Plane

A line is inclined at Φ to a plane. The vector equation of the line is given by \(\vec{r}\) = \(\vec{a}\) + λ \(\vec{b}\) and the vector equation of the plane can be given by \(\vec{r}.\hat{n}\) = d

Let θ be the angle between the line and the normal to the plane. Its value can be given by the following equation:

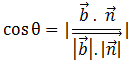
Φ is the angle between the line and the plane which is the complement of θ or 90 – θ. We know that cos θ is equal to sin (90 – θ). So Φ can be given by:

sin (90 – θ) = cos θ

or

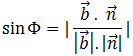
or

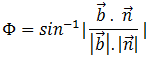
Example

Let us take up an example to understand the equations better.

Problem: A line has an equation \(\frac{x}{6}\) = \(\frac{y + 32}{2}\) = \(\frac{z – 2}{3}\). The equation of a plane is 3x + 4y – 12z = 7. Find the angle between them.

Solution: Let θ be the angle between the line and the normal to the plane. In the vector form, the equations can be written as:

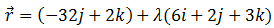
The equation of the plane in the vector form can be given by:

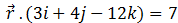
So we have \(\vec{b}\) = 6i + 2j + 3k and \(\vec{n}\) = 3i + 4j – 12k

Finding the value of the Φ between the line and the plane:

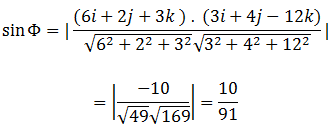
The value of Φ can be found by

To solve more examples and to watch video lectures on this topic, download BYJU’S The Learning App.