Bijective Function
In Mathematics, a bijective function is also known as bijection or one-to-one correspondence function. The term one-to-one correspondence should not be confused with the one-to-one function (i.e.) injective function. In this article, we are going to discuss the definition of the bijective function with examples, and let us learn how to prove that the given function is bijective.
What is Bijective Function?
A function is said to be bijective or bijection, if a function f: A → B satisfies both the injective (one-to-one function) and surjective function (onto function) properties. It means that every element “b” in the codomain B, there is exactly one element “a” in the domain A. such that f(a) = b. If the function satisfies this condition, then it is known as one-to-one correspondence.
Bijective Function Properties
A function f: A → B is a bijective function if every element b ∈ B and every element a ∈ A, such that f(a) = b. It is noted that the element “b” is the image of the element “a”, and the element “a” is the preimage of the element “b”. The basic properties of the bijective function are as follows:
While mapping the two functions, i.e., the mapping between A and B (where B need not be different from A) to be a bijection,
- each element of A must be paired with at least one element of B,
- no element of A may be paired with more than one element of B,
- each element of B must be paired with at least one element of A, and
- no element of B may be paired with more than one element of A.
Difference between Injective, Surjective, and Bijective Function
The difference between injective, surjective and bijective functions are given below:
| S.No | Injective Function | Surjective Function | Bijective Function |
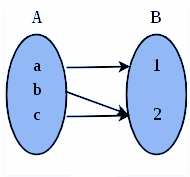
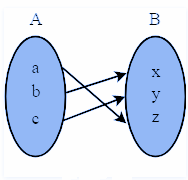
| 1 | A function that always maps the distinct element of its domain to the distinct element of its codomain | A function that maps one or more elements of A to the same element of B | A function that is both injective and surjective |
| 2 | It is also known as one-to-one function | It is also known as onto function | It is also known as one-to-one correspondence |
| 3 | 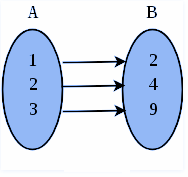 |
 |
 |
How to Prove that the Functions are Bijective?
Here, let us discuss how to prove that the given functions are bijective. If we want to find the bijections between two, first we have to define a map f: A → B, and then show that f is a bijection by concluding that |A| = |B|. To prove f is a bijection, we should write down an inverse for the function f, or shows in two steps that
- f is injective
- f is surjective
If two sets A and B do not have the same size, then there exists no bijection between them (i.e.), the function is not bijective. It is therefore often convenient to think of a bijection as a “pairing up” of the elements of domain A with elements of codomain B. In fact, if |A| = |B| = n, then there exists n! bijections between A and B.
Practice with: Relations and Functions Worksheets
Bijective Function Example
Example:
Show that the function f(x) = 3x – 5 is a bijective function from R to R.
Solution:
Given Function: f(x) = 3x – 5
To prove: The function is bijective.
According to the definition of the bijection, the given function should be both injective and surjective.
(i) To Prove: The function is injective
In order to prove that, we must prove that f(a)=c and f(b)=c then a=b.
Let us take,
f(a)=c and f(b)=c
Therefore, it can be written as:
c = 3a-5 and c = 3b-5
Thus, it can be written as:
3a-5 = 3b -5
Simplify the equation; we will get
a = b
Thus, the given function is injective
(ii) To Prove: The function is surjective
To prove this case, first, we should prove that that for any point “a” in the range there exists a point “b” in the domain s, such that f(b) =a
Let, a = 3x -5
Therefore, b must be (a+5)/3
Since this is a real number, and it is in the domain, the function is surjective.
Thus, the given function satisfies the condition of one-to-one function, and onto function, the given function is bijective.
Hence, proved.
To learn more Maths-related topics, register with BYJU’S -The Learning App and download the app to learn with ease.