Bisector
In Geometry, “Bisector” is a line that divides the line into two different or equal parts. It is applied to the line segments and angles. A line that passes through the midpoint of the line segment is known as the line segment bisector whereas the line that passes through the apex of an angle is known as angle bisector. In this article, let us discuss the definition of a bisector, its types, what is perpendicular bisector, constructions in detail.
Bisector Definition
The bisector is a line that divides a line or an angle into two equivalent parts. The bisector of a segment always contains the midpoint of the segment. There are two types of bisectors based on what geometrical shape it bisects.
- Line Segment Bisector (Perpendicular Bisector Theorem)
- Angle Bisector (Triangle Bisector Theorem)
Line Segment Bisector
A line segment bisector divides the line segment into 2 equal parts. It passes through the midpoint of the line segment. In the below figure line PQ is the bisector of AB.
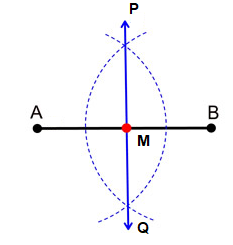
Example of Line Segment Bisector: Consider a line AB = 4cm. A line segment bisector will cut it into two equal parts of 2cm each.
If a bisector cuts the line segment into two equal parts at 90o, then the bisector is known as perpendicular bisector. Now, let us have a look at what is perpendicular bisector, how to construct the perpendicular bisector in detail.
What is Perpendicular Bisector?
A perpendicular bisector is a line segment or a ray or a line which intersects a given line segment at a 90o, and also it passes through the midpoint of the line segment. Two lines are said to be perpendicular to each other when they intersect in such a way that they form 90 degrees with each other. A bisector divides a line into two equal halves. Thus, when we talk about the perpendicular bisector of a line segment AB, it implies:
- It divides AB into two equal halves or bisects it.
- It makes right angles with (or is perpendicular to) AB.
- Every point in the perpendicular bisector is equidistant from point A and B.
Perpendicular Bisector Theorem
If a point is equidistant from the endpoints of the segment, then it lies on the perpendicular bisector of a segment.
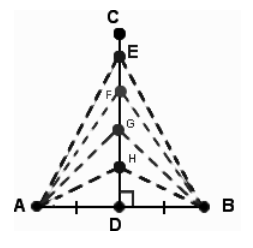
As given in the figure above: AH = BH, AG = BG, AF = BF and AE = BE.
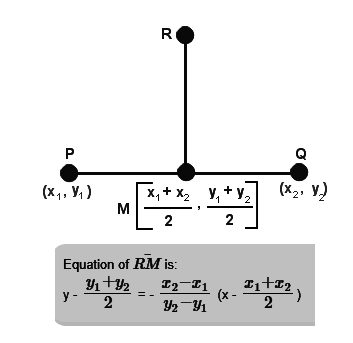
Perpendicular Bisector Equation
The equation of the perpendicular bisector of the segment joining the points (x1,y1) and (x2,y2)
How to Construct a Perpendicular Bisector?
You will require a ruler and compasses. The steps for the construction of a perpendicular bisector of a line segment are:
- Step 1: Draw a line segment PQ.
- Step 2: Adjust the compass with length a little more than half of the length of PQ.
- Step 3: Place the compass pointer at point P and draw arcs above and below the line.
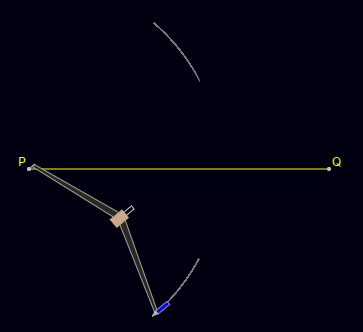
- Step 4: Keeping the same length in the compass, place the compass pointer at point Q. Similarly, draw two arcs above and below the line keeping the compass pointer at Q.
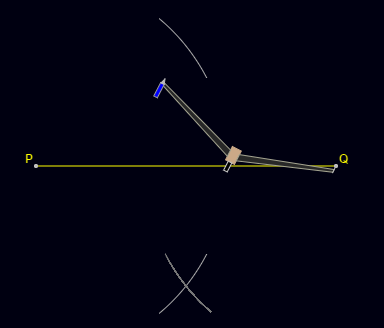
- Step 5: Mark the points where the opposite arcs cross as X and Y.
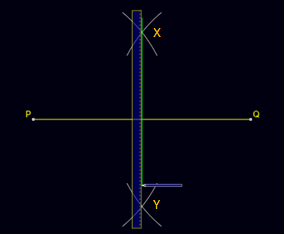
- Step 6: Using a ruler, draw a line passing across X and Y.
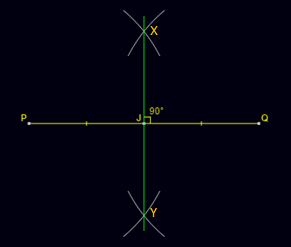
The perpendicular bisector bisects PQ at a point J, that is, the length PJ is equal to JQ. And the angle between the two lines is 90 degrees.
Angle Bisector
An angle bisector divides an angle into equal angles. If the angle is po, the two angles made will be (p/2)o. This angle bisector passes through the vertex of an angle, as shown in the figure.
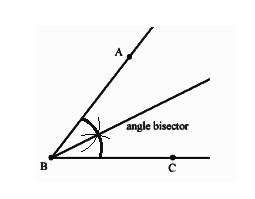
Example of Angle Bisector: Consider an Angle ∠ABC = 900. An angle bisector will cut it into two equal angles of 450 each.
Angle Bisector Theorem
If an angle bisector of an angle ∠A in a triangle ABC divides the opposite side in the same ratio as the sides adjacent to the angle, it will be called as Angle Bisector. For more details, check our angle bisector theorem
- Angle Bisector Conjecture – If a point is on the bisector of an angle is equidistant from the sides of the angle, it will be angle bisector conjecture.
Angle Bisector Example
An example of an angle bisector is a triangle bisector theorem which describes the perpendicular bisector of a triangle. A bisector which bisects any angle of a triangle is known as triangle bisector. It is a line segment which has its other endpoint on the opposite side of the angle which is bisected.
Triangle Bisector Theorem
Triangle Bisector theorem states that an angle bisector of an angle of a triangle will divide the opposite side into segments which are proportional to the other adjacent sides. In the below-given figure, AB/AC =BD/DC
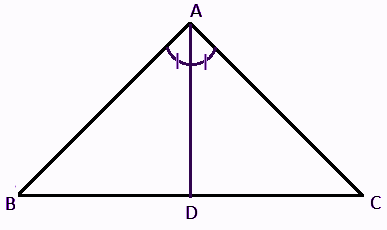
Angle Bisector Problem
Question:
What will be the value of x, if BD is the angle which bisects the ∠ABC in two equal angles?
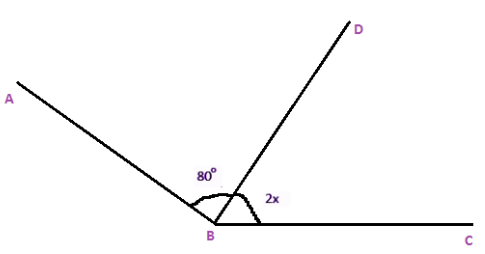
Solution:
As BD is the angle bisector of ∠ABC, so 2x = 80o, then x = 40o(By dividing each side by 2).
So, the value of x is 40o.
Register with BYJU’S – The Learning App and download the app to learn Maths-related articles with ease.