Class 9 Maths Chapter 6 Lines and Angles MCQs
Class 9 Maths Chapter 6 Lines and Angles MCQs are given here online with correct answers. The MCQs are prepared for Class 9 students as per the latest exam pattern. Students can practise these objective questions and test their problem-solving skills. All the multiple-choice questions are based on the latest CBSE syllabus (2021-2022) and the NCERT curriculum. Solving these chapter-wise problems will help students to score good marks. Also, check Important Questions for Class 9 Maths.
MCQs on Class 9 Maths Chapter 6 Lines and Angles
Below are the MCQs for Chapter 6 Lines and Angles of the 9th Standard. Each question has four options, among which one is the correct answer. Cross-check your answers with the one provided here.
1) A line joining two endpoints is called:
a. Line segment
b. A ray
c. Parallel lines
d. Intersecting lines
Answer: a
2) An acute angle is:
a. More than 90 degrees
b. Less than 90 degrees
c. Equal to 90 degrees
d. Equal to 180 degrees
Answer: b
3) A reflex angle is:
a. More than 90 degrees
b. Equal to 90 degrees
c. More than 180 degrees
d. Equal to 180 degrees
Answer: c
4) A straight angle is equal to:
a. 0°
b. 90°
c. 180°
d. 360°
Answer: c
5) Two angles whose sum is equal to 180° are called:
a. Vertically opposite angles
b. Complementary angles
c. Adjacent angles
d. Supplementary angles
Answer: d
6) Intersecting lines cut each other at:
a. One point
b. Two points
c. Three points
d. Null
Answer: a
Explanation: Two lines always intersect each other at one point.
7) Two parallel lines intersect at:
a. One point
b. Two points
c. Three points
d. Null
Answer: d
Explanation: If two lines are parallel to each other, they don’t intersect each other.
8) If two lines intersect each other, then the vertically opposite angles are:
a. Equal
b. Unequal
c. Cannot be determined
d. None of the above
Answer: a
Explanation: If two lines intersect each other, then the angles formed at the point of intersection are vertically opposite angles and are equal.
9) In the figure below, which of the following are corresponding angle pairs?

a. ∠p and ∠q
b. ∠p and ∠w
c. ∠p and ∠x
d. ∠p and ∠z
Answer: b
10) If AB || CD, EF ⊥ CD and ∠GED = 135° as per the figure given below.
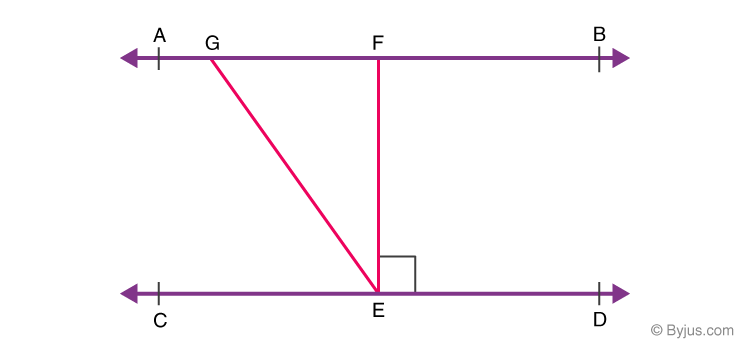
The value of ∠AGE is:
a. 120°
b. 140°
c. 90°
d. 135°
Answer: d
Explanation: Since AB || CD and GE is transversal.
Given, ∠GED = 135°
Hence, ∠GED = ∠AGE = 126° (Alternate interior angles)
11) An exterior angle of a triangle is 105° and its two interior opposite angles are equal. Each of these equal angles is
(a) 37 ½°
(b) 72 ½°
(c) 75°
(d) 52 ½°
Answer: d
Explanation:
The exterior angle of triangle = 105°
Let the interior angles be “x”.
By using, exterior angle theorem, Exterior angle = Sum of interior opposite angles
Therefore, 105° = x+x
2x = 105°
x = 52 ½°
12) If one of the angles of a triangle is 130°, then the angle between the bisectors of the other two angles can be
(a) 50°
(b) 65°
(c) 145°
(d) 155°
Answer: d
Explanation:
Assume a triangle ABC, such that ∠BAC=130°
Also, the bisectors of ∠B and ∠C meet at O.
To find: ∠BOC
In a triangle △ABC,
∠BAC+∠ABC+∠ACB=180°
By using the angle sum property of the triangle,
130°+∠ABC+∠ACB=180°
∠ABC+∠ACB=50°
½ (∠ABC+∠ACB)=25°
Since OB and OC bisect ∠ABC and ∠ACB
∠OBC+ ∠OCB=25°
Now, consider △OBC,
∠OBC+ ∠OCB+∠BOC=180°
25°+∠BOC=180°
∠BOC=155°
13) If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2 : 3, then the greater of the two angles is
(a) 54°
(b) 108°
(c) 120°
(d) 136°
Answer: b
Explanation: Consider the following figure,

Here, line AB is parallel to the line CD and t is the transversal.
Here, ∠1 and ∠2 are on the same side of the transversal. Hence, ∠1: ∠2 = 2:3
Let ∠1 = 2x and ∠2 = 3x.
Therefore, ∠1+∠2 = 180° (If a transversal intersects two parallel lines, each pair of consecutive angles are supplementary)
On substituting ∠1 = 2x and ∠2 = 3x in the above equation, we get
2x+3x = 180°
5x = 180°
x = 180°/5 = 36°
Hence, 3x >2x. It means ∠2 >∠1
The value of ∠2 = 3(36°) = 108°
14) If one angle of a triangle is equal to the sum of the other two angles, then the triangle is
(a) a right triangle
(b) an isosceles triangle
(c) an equilateral triangle
(d) an obtuse triangle
Answer: a
Explanation: If one angle of a triangle is equal to the sum of the other two angles, then the triangle is a right triangle. We know that the sum of interior angles of a triangle is equal to 180°. In the right triangle, one angle should be equal to 90°, and the remaining two angles are acute angles, and their sum is equal to 90°.
15) The angles of a triangle are in the ratio 5 : 3: 7. The triangle is
(a) a right triangle
(b) an acute-angled triangle
(c) an obtuse-angled triangle
(d) an isosceles triangle
Answer: b
Explanation: If the angles are in the ratio of 5:3:7, then a triangle is an acute angle triangle.
We know that the sum of the interior angles of a triangle is 180°
Therefore, 5x+3x+7x = 180°
15x = 180°
x = 180°/15 = 12°
Thus, 5x = 5(12°) =60°
3x = 3(12°) =36°
7x = 7(12°) =84°
Since all the angles are less than 90°, the triangle is an acute angle triangle.
16) Angles of a triangle are in the ratio 2: 4 : 3. The smallest angle of the triangle is
(a) 20°
(b) 40°
(c) 60°
(d) 80°
Answer: b
Explanation:
We know that the sum of the interior angles of a triangle is 180°
Given that, the angles of a triangle are in the ratio of 2:4:3
Hence, 2x+4x+3x = 180°
9x = 180°
x= 20°
Therefore,
2x = 2(20) = 40°
4x = 4(20) = 80°
3x = 3(20) = 60°
Hence, the angles are 40°, 80° and 60°.
Therefore, the smallest angle of a triangle is 40°.
17) In the given figure, POQ is a line. The value of x is
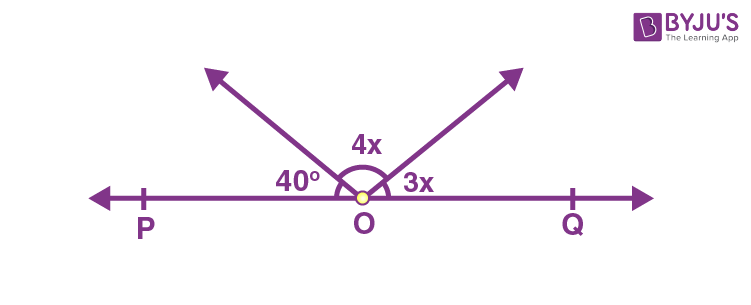
(a) 20°
(b) 25°
(c) 30°
(d) 35°
Answer: a
Explanation:
Given that POQ is a line. Hence, POQ = 180°
Therefore, 40°+4x+3x = 180°
7x = 180°-40°
7x = 140°
x = 140°/7
x = 20°
Hence, the value of x is 20°.
18) In the given figure, , if AB || CD || EF, PQ || RS, ∠RQD = 25° and ∠CQP = 60°, then ∠QRS is equal to

(a) 85°
(b) 110°
(c) 135°
(d) 145°
Answer: d
Explanation: Given that, AB || CD || EF, PQ || RS, ∠RQD = 25° and ∠CQP = 60°.
To find: ∠QRS.
∠SRB=∠CQP=60° (or)
∠QRA =∠RQD=25°
Therefore, ∠ARS+∠SRB=180°
∠ARS = 180°- 60°
∠ARS = 120°
Hence, ∠QRS = ∠ARS+∠QRA = 120°+25°
∠QRS = 145°
19) An obtuse angle is
(a) Less than 90°
(b) Greater than 90°
(c) Equal to 90°
(d) Equal to 180°
Answer: b
Explanation: An obtuse angle is an angle that is greater than 90°
20) In the given figure, if OP||RS, ∠OPQ = 110° and ∠QRS = 130°, then ∠PQR is equal to
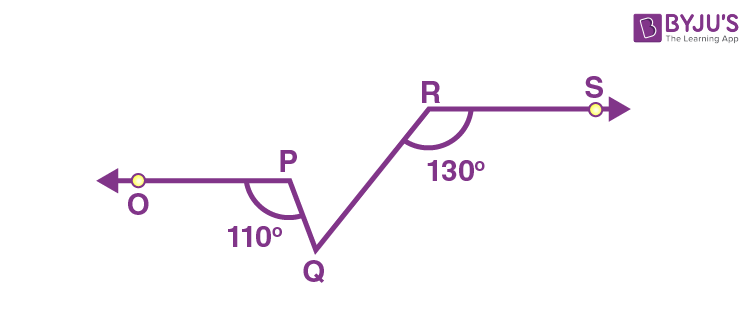
(a) 40°
(b) 50°
(c) 60°
(d) 70°
Answer: c
Explanation:
Now, consider the figure,
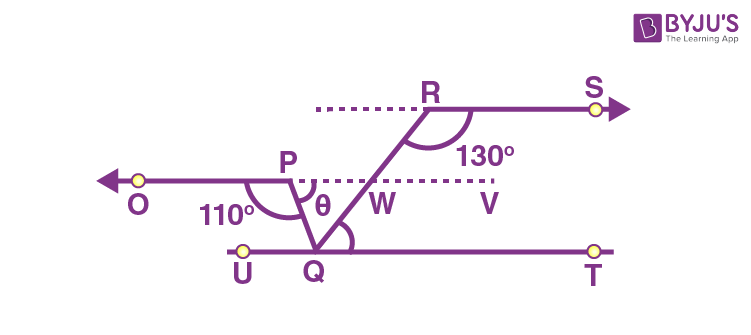
Using, OP || RS, we know that
∠RWV = 180°- 130°
Hence, ∠RWV = 50°
Since opposite angles of intersecting lines are equal,
∠PWQ = ∠RWV = 50°
For line OP
∠OQP + θ = 180°
θ = 180° – ∠OPQ = 180° − 110°
θ = 70°
Now, by using the fact, that the sum of interior angles of a triangle is 180°, we can write
∠PQR + θ + ∠PWQ = 180°
∠PQR = 180°- θ – ∠PWQ = 180°- 70°- 50°
∠PQR = 180° − 120°
∠PQR = 60°
Hence, ∠PQR is equal to 60°.
Related Articles for Class 9
- Lines and Angles Introduction
- Lines and Angles Class 9
- Lines and Angles Worksheet
- Important Questions Class 9 Maths Chapter 6-Lines and Angles
Stay tuned with BYJU’S – The Learning App and download the app today to get more class-wise concepts.