Cbse Class 10 Maths Important 4 Marks Questions
Maths requires skills and understanding rather than just memorizing. As every other subject requires knowledge where memorization technique works fine, but for the subject of mathematics, it requires in-depth conceptual understanding.
We at BYJU’S provide students of class 10th with important 4 marks questions so that students can practice them. Students can get a replica of these questions, provided here, in their board examination.
Students preparing for CBSE Class 10 Maths Board Examination can go through the important 4 marks questions and solutions given below and practice the additional questions provided at the end to excel in their problem-solving skills.
Important 4 Marks Questions and Solutions for Class 10 Maths Board are as follows-
Question 1- Solve for x:
\(\frac{1}{x-2} + \frac{2}{x – 1} = \frac{6}{x},\)
\(x \neq 0, 1, 2\)
Solution:
\(\frac{1}{x-2}+\frac{2}{x-1}=\frac{6}{x}\)
Taking LCM and cross multiplying the terms,
\(\frac{(x-1)+2(x-2)}{(x-1)(x-2)}=\frac{6}{x}\)
x[x – 1 + 2x – 4] = 6[x2 – 2x – x + 2]
x(3x – 5) = 6(x2 – 3x + 2)
6x2 – 18x + 12 – 3x2 + 5x = 0
3x2 – 13x + 12 = 0
3x2 – 9x – 4x + 12 = 0
3x(x – 3) – 4(x – 3) = 0
(3x – 4)(x – 3) = 0
3x – 4 = 0, x – 3 = 0
x = 4/3, 3
Question 2-
Find the sum of first 24 terms of an A.P. whose nth term is given by \(a_{n} = 3 + 2n\).
Solution:
Given,
an = 3 + 2n
Substituting n = 1, 2, 3,…
When n = 1,
a1 = 3 + 2(1) = 3 + 2 = 5
When n = 2,
a2 = 3 + 2(2) = 3 + 4 = 7
When n = 3,
a3 = 3 + 2(3) = 3 + 6 = 9
Thus, the AP is: 5, 7, 9,…
Here,
First term = a = 5
Common difference = d = 2
We know that,
Sum of first n terms of an AP = Sn = (n/2) [2a + (n – 1)d]
Now,
S24 = (24/2) [2(5) + (24 – 1)(2)]
= 12[10 + 23(2)]
= 12[10 + 46]
= 12 × 56
= 672
Therefore, the sum of the first 24 terms of the given AP is 672.
Question 3-
A bucket, is in the form of a frustum of a cone whose height is 42 cm and the radii of its circular ends are 30 cm and 10 cm. Find the amount of milk (in litres) which this bucket can hold. If the milkman sells the milk at the rate of Rs. 40 per litre, what amount he will get from the sale?
If the milkman sells half the milk at less rate to the economically weaker section of society, what value he exhibits by doing this?
Solution:
Given that a bucket is in the form of a frustum of a cone with the following dimensions.
Height = h = 42 cm
R = 30 cm
r = 10 cm
Volume of frustum of a cone = (1/3)πh[R2 + r2 + Rr]
Substituting the values,
= (1/3) × (22/7) × 42 × [(30)2 + (10)2 + (30)(10)]
= 44 × [900 + 100 + 300]
= 44 × 1300
= 572000 cm3
= (572000/1000) litres {since 1 cm3 = 1/1000 litres}
= 57.2 litres
Therefore, the bucket can hold 57.2 litres of milk.
Also,
Cost of 1 litre milk = Rs. 40 (given)
So, the cost of 57.2 litres of milk = 57.2 × Rs. 40 = Rs. 2288
Hence, the milkman can get Rs. 2288 from selling the milk in the bucket.
If the milkman sells half the milk at less rate to the economically weaker section of society, he shows the values of help, kindness, and empathy.
Question 4-
If the coordinates of two points are A(3,4), B (5,-2) and a point P (x,5) is such that PA = PB, then find the area of \(\Delta PAB\).
Solution:
Given points:
A(3, 4), B(5, -2) and P(x, 5)
Also,
PA = PB
Squaring on both sides,
PA2 = PB2
Using distance formula, d = √[(x2 – x1)2 + (y2 – y1)2];
(x – 3)2 + (5 – 4)2 = (x – 5)2 + (5 + 2)2
x2 + 9 – 6x + 1 = x2 + 25 – 10x + 49
10 – 6x = 74 – 10x
⇒ 10x – 6x = 74 – 10
⇒ 4x = 64
⇒ x = 16
⇒P = (x, 5) = (16, 5)
Let,
P(16, 5) = (x1, y1), A(3, 4) = (x2, y2), B(5, -2) = (x3, y3)
Area of triangle PAB = (1/2)|x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)|
= (1/2)|16(4 + 2) + 3(-2 – 5) + 5(5 – 4)|
= (1/2)|16(6) + 3(-7) + 5(1)|
= (1/2)|96 – 21 + 5|
= (1/2) × 80
= 40 square units
Question 5-
A solid metallic cylinder of diameter 12 cm and height 15 cm is melted and recast into toys in the shape of a cone of radius 3 cm and height 9 cm. Find the number of toys so formed.
Solution:
Given,
Height of cylinder = H = 15 cm
Diameter = 12 cm
Radius of cylinder = R = 12/2 = 6 cm
Radius of cone = 3 cm
Height of cone = h = 9 cm
Let n be the number of toys in the shape of a cone made.
So,
Volume of cylinder = n × volume of a cone
πR2H = (1/3)πr2h
6 × 6 × 15 = n × (1/3) × 3 × 3 × 9
n = (6 × 6 × 15 × 3)/(3 × 3 × 9)
n = 20
Question 6-
From a pack of 52 playing cards, Jacks and Kings of red colour and Queens and Aces of black colour are removed. The remaining cards are mixed and a card is drawn at random. Find the probability that the drawn card is
(i) a black Queen
(ii) a card of red colour
(iii) a Jack of black colour
(iv) a face card
Solution:
We know that, P(an event) = Number of favourable outcomes/Total number of outcomes
Given,
From a pack of 52 playing cards, Jacks and Kings of red colour and Queens and Aces of black colour are removed.
So, the total number of outcomes = 52 – (2 + 2 + 2 + 2) = 52 – 8 = 44
(i) a black Queen
Number of black queen cards in the available cards = 0
P(getting a black queen) = 0/44 = 0
(ii) a card of red colour
Number of red colour cards = 26 – 4 = 22
P(getting a card of red colour) = 22/44 = 1/2
(iii) a Jack of black colour
Number of black Jack cards = 2
P(getting a Jack of black colour) = 2/44 = 1/22
(iv) a face card
Number of face cards = 12 – 6 = 6
P(getting a face card) = 6/44 = 3/22
Question 7-
From a point P on the ground, the angles of elevation of the top of a 10 m tall building and a helicopter, hovering at some vertically over the top the building is \(30^{\circ}\) and \(60^{\circ}\) respectively. Find the height of the helicopter above the ground.
Solution:
Let P be the position of a point and C be the position of a helicopter.
Height of the building AB = 10 m
AC = x m
PA = y m
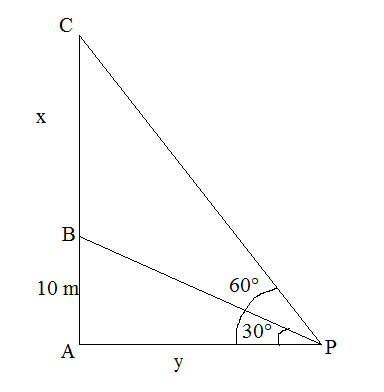
In right triangle PAB,
tan 30° = AB/PA
1/√3 = 10/y
y = 10√3 m
In right triangle PAC,
tan 60° = AC/PA
√3 = (x + 10)/10√3
10√3 √3 = x + 10
x = 30 – 10 = 20
Therefore, the height of helicopter from the ground = x + 10 = 20 + 10 = 30 m
Question 8-
Draw a line segment AB of length 7 cm. Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each circle from the centre of the other circle.
Solution:
Steps of Construction:
Step 1: Draw a line segment AB of 7 cm.
Step 2: Taking A and B as centres, draw two circles of 3 cm and 2 cm radius respectively.
Step 3: Bisect the line AB. Let the midpoint of AB be C.
Step 4: Taking C as centre, draw a circle of radius AC which intersects the two circles at point P,Q,R and S.
Step 5: Join BP, BQ, AS and AR.
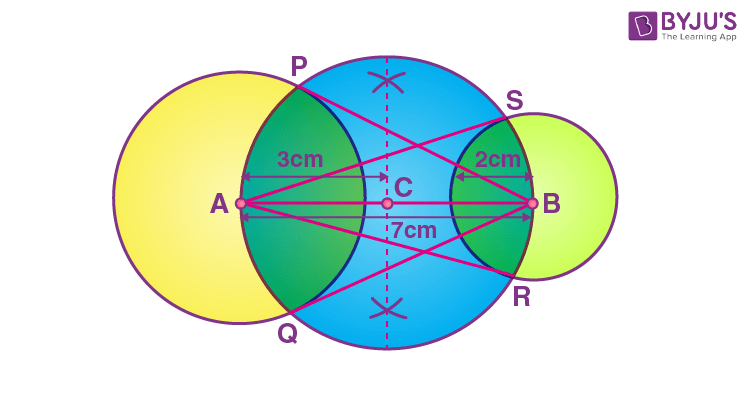
Here, BP, BQ, AS and AR are the tangents to the circles.
Question 9-
Prove that the lengths of tangents drawn from an external point to a circle are equal.
Solution:
Consider a circle with the centre “O” and P is the point that lies outside the circle. Hence, the two tangents formed are PQ and PR.
We need to prove: PQ = PR.
To prove the tangent PQ is equal to PR, join OP, OQ and OR. Hence, ∠OQP and ∠ORP are the right angles.
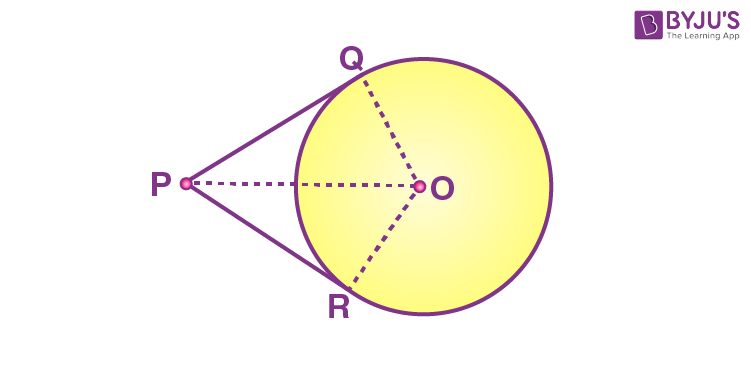
Therefore, OQ = OR (Radii)
OP = OP (Common side)
By using the RHS rule, we can say, ∆ OQP ≅ ∆ ORP.
Thus, by using the CPCT rule, the tangent PQ = PR.
Hence proved.
Question 10-
The Life insurance agent found the following data for the distribution of ages of 100 policyholders. Calculate the median age, if policies are given only to the persons whose age is 18 years onwards but less than the 60 years.
| Age (in years) | Number of policyholders |
| Below 20 | 2 |
| Below 25 | 6 |
| Below 30 | 24 |
| Below 35 | 45 |
| Below 40 | 78 |
| Below 45 | 89 |
| Below 50 | 92 |
| Below 55 | 98 |
| Below 60 | 100 |
Solution:
Let us calculate the class intervals and the corresponding frequencies for the given data.
| Class interval | Frequency | Cumulative frequency |
| 15 – 20 | 2 | 2 |
| 20 – 25 | 4 | 6 |
| 25 – 30 | 18 | 24 |
| 30 – 35 | 21 | 45 |
| 35 – 40 | 33 | 78 |
| 40 – 45 | 11 | 89 |
| 45 – 50 | 3 | 92 |
| 50 – 55 | 6 | 98 |
| 55 – 60 | 2 | 100 |
N = 100
N/2 = 100/2 = 50
The cumulative frequency greater than and nearer to 50 is 78 which belongs to the class interval 35 – 40.
So, the median class is 35 – 40.
Frequency of the median class = f = 33
Lower limit of median class = l = 35
Cumulative frequency of the class preceding the median class = cf = 45
Class size = h = 5
Median = l + [(N/2 – cf)/f] × h
= 35 + [(50 – 45)/33] × 5
= 35 + (25/33)
= 35 + 0.75
= 35.75 (approx.)
Therefore, the median age = 35.75 years.
CBSE Class 10 Maths Important 4 Marks Questions for Practice
- Draw an isosceles triangle ABC in which the base BC is 8 cm long and its altitude AD through A is 4 cm long. Then draw another triangle whose side is \(\frac{2}{3}\) of the corresponding sides of \(\Delta ABC\).
- Prove that √5 is an irrational.
- A hollow metallic sphere of external and internal diameters 8 cm and 4 cm respectively is melted to form a solid cone of base diameter 8 cm. Find the height of the cone.
- Find the area of the triangle formed by joining the mid-points of sides of triangle vertices (2,1), (4,3) and (2,5).
- Prove that the parallelogram circumscribing a circle is a rhombus.
- A sum of Rs. 4000 is to be used to give 10 cash prizes to students of a school, for their overall academic performance. If each prize is Rs. 50 less than its preceding prize, find the value of each prize.
- Find the sum of all such multiples of 7 which are less than 500.
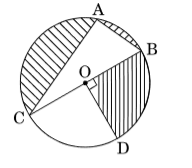
- In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and \(\angle BOD = 90^{\circ}\). Find the area of the shaded region.
- On dividing p(x) = x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were (x – 2) and (–2x + 4), respectively. Find g(x).
- In a rain-water harvesting system, the rain-water from a roof of 22 m \(\times\) 20 m drains into a cylindrical tank having a diameter of base 2 m and height 3.5 m. If the tank is full, find the rainfall in cm. Write your views on water conservation.
To practice more questions, students must solve the CBSE board sample papers for class 10. Stay tuned for further updates on CBSE and other competitive exams. To access interactive Maths and Science videos download BYJU’S – The Learning App.