Compound Interest
Compound interest is the interest imposed on a loan or deposit amount. It is the most commonly used concept in our daily existence. The compound interest for an amount depends on both Principal and interest gained over periods. This is the main difference between compound and simple interest.
Suppose we observe our bank statements, we generally notice that some interest is credited to our account every year. This interest varies with each year for the same principal amount. We can see that interest increases for successive years. Hence, we can conclude that the interest charged by the bank is not simple interest; this interest is known as compound interest or CI. In this article, you will learn what CI is, formula and derivation of formula to calculate the CI when compounded annually, half-yearly, quarterly, etc. Also, one can understand why the return on compound interest is more than the return on simple interest through the examples given based on real-life applications of CI here.
| Table of Contents: |
Compound Interest Definition
Compound interest is the interest calculated on the principal and the interest accumulated over the previous period. It is different from simple interest, where interest is not added to the principal while calculating the interest during the next period. In Mathematics, compound interest is usually denoted by C.I.
Compound interest finds its usage in most of the transactions in the banking and finance sectors and other areas. Some of its applications are:
- Increase or decrease in population.
- The growth of bacteria.
- Rise or Depreciation in the value of an item.
Compound Interest in Maths
In Maths, Compound interest can be calculated in different ways for different situations. We can use the interest formula of compound interest to ease the calculations. To calculate compound interest, we need to know the amount and principal. It is the difference between amount and principal.
Compound Interest Formula
As we have already discussed, the compound interest is the interest-based on the initial principal amount and the interest collected over the period of time. The compound interest formula is given below:
Compound Interest = Amount – Principal
Here, the amount is given by:

Where,
- A = amount
- P = principal
- r = rate of interest
- n = number of times interest is compounded per year
- t = time (in years)
Alternatively, we can write the formula as given below:
CI = A – P
And
\(CI=P\left ( 1+\frac{r}{n} \right )^{nt}-P\)
This formula is also called periodic compounding formula.
Here,
- A represents the new principal sum or the total amount of money after compounding period
- P represents the original amount or initial amount
- r is the annual interest rate
- n represents the compounding frequency or the number of times interest is compounded in a year
- t represents the number of years
It is to be noted that the above formula is the general formula for the number of times the principal is compounded in a year. If the interest is compounded annually, the amount is given as:
\(A = P \left (1 + \frac{R}{100} \right )^t\)
Thus, the compound interest rate formula can be expressed for different scenarios such as the interest rate is compounded yearly, half-yearly, quarterly, monthly, daily, etc.
Interest Compounded for Different Years
Let us see, the values of Amount and Interest in case of Compound Interest for different years-
| Time (in years) | Amount | Interest |
| 1 | P(1 + R/100) | \(\frac{PR}{100}\) |
| 2 | \(P\left (1+\frac{R}{100} \right )^{2}\) | \(P\left (1+\frac{R}{100} \right )^{2}-P\) |
| 3 | \(P\left (1+\frac{R}{100} \right )^{3}\) | \(P\left (1+\frac{R}{100} \right )^{3}-P\) |
| 4 | \(P\left (1+\frac{R}{100} \right )^{4}\) | \(P\left (1+\frac{R}{100} \right )^{4}-P\) |
| n | \(P\left (1+\frac{R}{100} \right )^{n}\) | \(P\left (1+\frac{R}{100} \right )^{n}-P\) |
The above formulas help determine the interest and amount in case of compound interest quickly.
| NOTE:
From the data, it is clear that the interest rate for the first year in compound interest is the same as that in simple interest. PR/100. Other than the first year, the interest compounded annually is always greater than that in simple interest. |
Derivation of Compound Interest Formula
To derive the formula for compound interest, we use the simple interest formula as we know SI for one year is equal to CI for one year (when compounded annually).
Let, Principal amount = \(P\), Time = \(n\) years, Rate = \(R\)
Simple Interest (SI) for the first year:
\(SI_1\) = \(\frac{P~×~R~×~T}{100}\)
Amount after first year = \(P~+~SI_1\)
= \(P ~+~ \frac{P~×~R~×~T}{100}\)
= \(P \left(1+ \frac{R}{100}\right)\) = \(P_2\)
Simple Interest (SI) for second year:
\(SI_2\) = \(\frac{P_2~×~R~×~T}{100}\)
Amount after second year = \(P_2~+~SI_2\)
= \(P_2 ~+~ \frac{P_2~×~R~×~T}{100}\)
= \(P_2\left(1~+~\frac{R}{100}\right)\)
= \(P\left(1~+~\frac{R}{100}\right) \left(1~+~\frac{R}{100}\right)\)
= \(P \left(1~+~\frac{R}{100}\right)^2\)
Similarly, if we proceed further to \(n\) years, we can deduce:
\(A\) = \(P\left(1~+~\frac{R}{100}\right)^n\)
\(CI\) = \(A~–~P\) = \(P \left[\left(1~+~ \frac{R}{100}\right)^n~ –~ 1\right]\)
Compound Interest when the Rate is Compounded half Yearly
Let us calculate the compound interest on a principal, P for 1 year at an interest rate R % compounded half-yearly.
Since interest is compounded half-yearly, the principal amount will change at the end of the first 6 months. The interest for the next six months will be calculated on the total amount after the first six months. Simple interest at the end of first six months,
\(SI_1\) = \(\frac{P~×~R~×~1}{100~×~2}\)
Amount at the end of first six months,
\(A_1\) = \(P~ + ~SI_1\)
= \(P ~+~ \frac{P~×~R~×~1}{2~×~100}\)
= \(P \left(1~+~\frac{R}{2~×~100}\right)\)
= \(P_2\)
Simple interest for next six months, now the principal amount has changed to \(P_2\)
\(SI_2\) = \(\frac{P_2~×~R~×~1}{100~×~2}\)
Amount at the end of 1 year,
\(A_2\) = \(P_2~ +~ SI_2\)
= \(P_2 ~+~ \frac{P_2~×~R~×~1}{2~×~100}\)
= \(P_2\left(1~+~\frac{R}{2~×~100}\right)\)
= \(P \left(1~+~\frac{R}{2~×~100}\right)\left(1~+~\frac{R}{2~×~100}\right)\)
= \(P \left(1~+~\frac{R}{2~×~100}\right)^2\)
Now we have the final amount at the end of 1 year:
\(A\) = \(P\left(1~+~\frac{R}{2~×~100}\right)^2\)
Rearranging the above equation,
\(A\) = \(P\left(1~+~\frac{\frac{R}{2}}{100}\right)^{2~×~1}\)
Let \(\frac{R}{2}\) = \(R'\); \(2T\) = \(T’\), the above equation can be written as, [for the above case \(T\) = \(1\) year]
\(A\) = \(P\left(1~+~\frac{R’}{100}\right)^{T’}\)
Hence, when the rate is compounded half-yearly, we divide the rate by 2 and multiply the time by 2 before using the general formula for compound interest.
Quarterly Compound Interest Formula
Let us calculate the compound interest on a principal, P kept for 1 year at an interest rate R % compounded quarterly. Since interest is compounded quarterly, the principal amount will change at the end of the first 3 months(first quarter). The interest for the next three months (second quarter) will be calculated on the amount remaining after the first 3 months. Also, interest for the third quarter will be calculated on the amount remaining after the first 6 months and for the last quarter on the remaining after the first 9 months. Thus the interest compounded quarterly formula is given by:
\(A=P(1+\frac{\frac{R}{4}}{100})^{4T}\)
CI = A – P
Or
\(CI =P(1+\frac{\frac{R}{4}}{100})^{4T}-P\)
Here,
A = Amount
CI = Compound interest
R = Rate of interest per year
T = Number of years
Formula for Periodic Compounding Rate
The total accumulated value, including the principal P plus compounded interest I, is given by the formula:
P’ = P[1 + (r/n)]nt
Here,
P = Principal
P’ = New principal
r = Nominal annual interest rate
n = Number of times the interest is compounding
t = Time (in years)
In this case, compound interest is:
How to Calculate Compound Interest?
Let us understand the process of calculating compound interest with the help of the below example.
Example: What amount is to be repaid on a loan of Rs. 12000 for one and half years at 10% per annum compounded half yearly?
Solution:
For the given situation, we can calculate the compound interest and total amount to be repaid on a loan in two ways. In the first method, we can directly substitute the values in the formula. In the second method, compound interest can be obtained by splitting the given time bound into equal periods.
This can be well understood with the help of the table given below.

Related Articles
- Simple Interest and Compound Interest
- Monthly compound interest formula
- Daily compound interest formula
- Compound Interest Calculator
- Simple interest formula
Compound Interest Solved Examples
As mentioned above, compound interest has many applications in real-life. Let us solve various examples based on these applications to understand the concept in a better manner.
Increase or Decrease in Population
| Examples 1:
A town had 10,000 residents in 2000. Its population declines at a rate of 10% per annum. What will be its total population in 2005? Solution: The population of the town decreases by 10% every year. Thus, it has a new population every year. So the population for the next year is calculated on the current year population. For the decrease, we have the formula A = P(1 – R/100)n Therefore, the population at the end of 5 years = 10000(1 – 10/100)5 = 10000(1 – 0.1)5 = 10000 x 0.95 = 5904 (Approx.) |
The Growth of Bacteria
| Examples 2:
The count of a certain breed of bacteria was found to increase at the rate of 2% per hour. Find the bacteria at the end of 2 hours if the count was initially 600000. Solution: Since the population of bacteria increases at the rate of 2% per hour, we use the formula A = P(1 + R/100)n Thus, the population at the end of 2 hours = 600000(1 + 2/100)2 = 600000(1 + 0.02)2 = 600000(1.02)2 = 624240 |
Rise or Depreciation in the Value of an Item
| Examples 3:
The price of a radio is Rs. 1400 and it depreciates by 8% per month. Find its value after 3 months. Solution: For the depreciation, we have the formula A = P(1 – R/100)n. Thus, the price of the radio after 3 months = 1400(1 – 8/100)3 = 1400(1 – 0.08)3 = 1400(0.92)3 = Rs. 1090 (Approx.) |
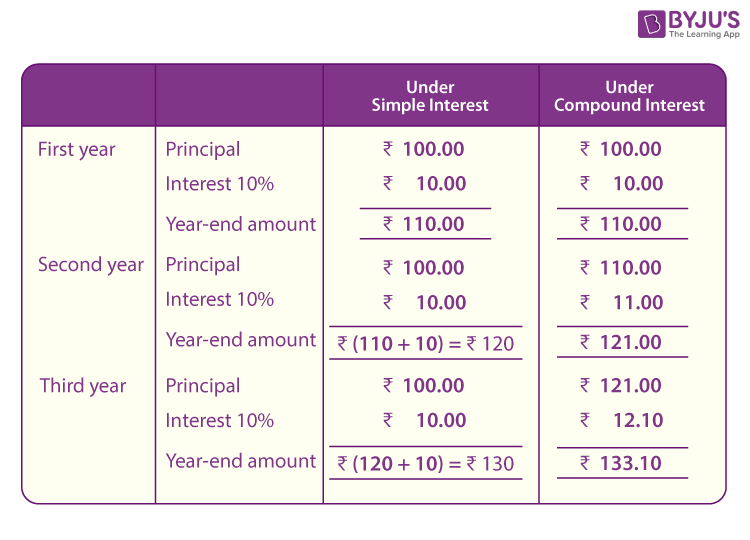
Compound Interest and Simple Interest
Now, let us understand the difference between the amount earned through compound interest and simple interest on a certain amount of money, say Rs. 100 in 3 years . and the rate of interest is 10% p.a.
Below table shows the process of calculating interest and total amount.
Compound Interest Word Problems
Question 1: A sum of Rs.10000 is borrowed by Akshit for 2 years at an interest of 10% compounded annually. Find the compound interest and amount he has to pay at the end of 2 years.
Solution:
Given,
Principal/ Sum = Rs. 10000, Rate = 10%, and Time = 2 years
From the table shown above it is easy to calculate the amount and interest for the second year, which is given by-
Amount(\(A_{2}\)) = \(P\left (1+\frac{R}{100} \right )^{2}\)
Substituting the values,
\(A_{2} = 10000 \left ( 1 + \frac{10}{100} \right )^{2} \\ = 10000 \left ( \frac{11}{10} \right )\left ( \frac{11}{10} \right )\\= Rs.12100\)Compound Interest (for 2nd year) = A2 – P = 12100 – 10000 = Rs. 2100
Question 2: What is the compound interest (CI) on Rs.5000 for 2 years at 10% per annum compounded annually?
Solution:
Principal (P) = Rs.5000 , Time (T)= 2 year, Rate (R) = 10 %
We have, Amount, \(A = P \left ( 1 + \frac{R}{100} \right )^{T}\)
\(A = 5000 \left ( 1 + \frac{10}{100} \right )^{2}\\ = 5000 \left ( \frac{11}{10} \right )\left ( \frac{11}{10} \right )\\ = 50 \times 121\\ = Rs. 6050\)
Interest (Second Year) = A – P = 6050 – 5000 = Rs.1050
OR
Directly we can use the formula for calculating the interest for the second year, which will give us the same result.
Interest (I1) = \(P\times \frac{R}{100} = 5000 \times \frac{10}{100} =500\)
Interest (I2) = \(P\times \frac{R}{100}\left (1 + \frac{R}{100} \right )\\ = 5000 \times \frac{10}{100}\left ( 1 + \frac{10}{100} \right )\\ = 550\)
Total Interest = I1+ I2 = 500 + 550 = Rs. 1050
Question 3: What is the compound interest to be paid on a loan of Rs.2000 for 3/2 years at 10% per annum compounded half-yearly?
Solution: From the given,
Principal \(P = Rs.2000\),
Time, \(T’=2\times \frac{3}{2}\) years = 3 years,
Rate, \(R’=\frac{10%}{2}=5%\),
Amount, \(A\) can be given as:
\(A = P(1+\frac{R’}{100})^{T’}\)\(A = 2000~×~\left(1~+~\frac{5}{100}\right)^3\)
\(=2000~×~\left(\frac{21}{20}\right)^3 \\ = Rs.2315.25\)
CI = A – P = Rs.2315.25 – Rs.2000 = Rs.315.25
Compound Interest Practice Problems
Try solving the below questions on compound interest.
- What is the least number of complete years in which a sum of money put out at 20% compound interest will be more than doubled?
- Heera invests Rs. 20,000 at the beginning of every year in a bank and earns 10 % annual interest, compounded at the end of the year. What will be her balance in the bank at the end of three years?
- What is the difference between the compound interests on Rs. 5000 for one and half years at 4% per annum compounded yearly and half-yearly?
For a detailed discussion on compound interest, download BYJU’S -The learning app.
Frequently Asked Questions (FAQs) on Compound Interest
What is Compound interest?
How do you calculate compound interest?
Here,
P = Initial amount
R = Annual rate of interest as a percentage
n = Number of compounding periods in a given time
Who benefits from compound interest?
What is interest compounded quarterly formula?
A = P(1 + (R/4)/100)4T
How do you find the compound interest rate?
A = P(1 + r/n)^{nt}
A = Total amount
P = Principal
r = Annual nominal interest rate as a decimal
n = Number of compounding periods
t = Time (in years)
Thus, compound interest (CI) = A – P
What is the formula of compound interest with an example?
Compound Interest = Amount – Principal
Where the amount is given by:
A = P(1 + r/n)^{nt}P = Principal
r = Annual nominal interest rate as a decimal
n = Number of compounding periods
t = Time (in years)
For example, If Mohan deposits Rs. 4000 into an account paying 6% annual interest compounded quarterly, and then the money will be in his account after five years can be calculated as:
Substituting, P = 4000, r = 0.06, n = 4, and t = 5 in A = A = P(1 + r/n)^{nt}, we get A = Rs. 5387.42
What is the compounded daily formula?
A = P(1 + r/365)^{365 * t}