Coordinates of A Point in Three Dimensions
In order to locate the position of a point in space, we require a rectangular coordinate system. After choosing a fixed coordinate system in 3D, the coordinates of any point P in that system can be given by an ordered 3-tuple (x, y, z). Also, if the coordinates ( x, y,z) are already known then we can easily locate the point P in space.
Three Dimensional Coordinate System
Let there be a point P in space as shown in the figure below. If we drop a perpendicular PB on the XY plane and then from point B, we drop perpendiculars BA and BC on the x-axis and y-axis respectively. Assuming the length of the perpendiculars BC, BA and PB as x, y and z respectively. These lengths x, y and z are known as the co-ordinates of the point P in three-dimensional space. It must be noted that while giving the coordinates of a point, we always write them in order such that the co-ordinate of x-axis comes first, followed by the co-ordinate of the y-axis and the z-axis. Thus for each point in space there exist an ordered 3-tuple of real numbers for its representation.
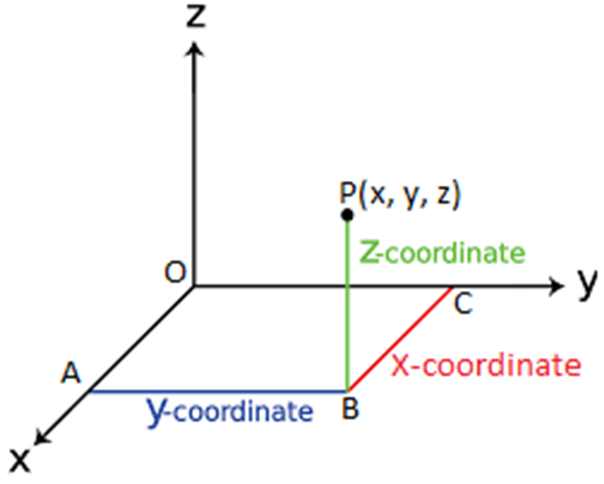
Figure 1 Co-ordinates of a point in space
In the figure given above the co-ordinates of P are given by (x, y, z). The coordinates of the origin O is (0, 0, 0) Also the coordinates of the point A is given by (x, 0, 0)as A lies completely on the x-axis. Similarly, the coordinates of any point on y-axis is given as (0, y, 0) and on the z-axis, the coordinates are given as (0, 0, z). Also the coordinates of any point in three planes XY, YZ and ZX will be (x,y,0), (0,y,z) and (x,0,z) respectively.
In questions, where we are asked to locate a point,i.e. when the co-ordinates of the point are given, then we have to draw three planes parallel to XY, YZ and ZX plane meeting the three axes in points A, B and C as shown in the figure. Let OA = x , OB = y and OC = z. Then the coordinates of the point are given as (x,y,z).
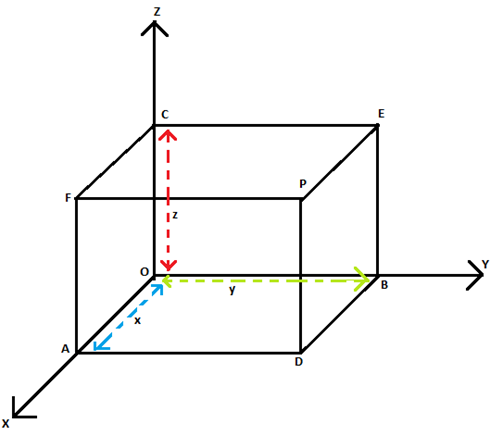
The planes ADPF, BDPE and CEPF intersect at point P which corresponds to the ordered triplet ( x, y, z).
To determine the octant in which a point lies, the signs of the coordinates of a point are helpful. The following table depicts the sign of the coordinates of a point and the octant in which it lies.
| Octants | I | II | III | IV | V | VI | VII | VIII |
| Co-ordinates | ||||||||
| x | + | – | – | + | + | – | – | + |
| y | + | + | – | – | + | + | – | – |
| z | + | + | + | + | – | – | – | – |
Using the above table we can easily figure out the signs of coordinates of a point or the octant in which it lies.
How to Plot the Points in Three-dimensional Plane?
The following points illustrate how to plot the points in the three-dimensional coordinate system:
- Locate the point “x” on the X-axis
- From the point x, moving parallel to the Y-axis, locate the point “y”.
- Similarly, from the determined point, moving parallel to the Z-axis, locate the point “z”.
- This is the final coordinate point in the three-dimensional plane, which we are looking for.
To learn more about three-dimensional geometry please visit our website www.byjus.com. Fall in love with learning.