Cuboid
In geometry, a cuboid is a solid shape or a three-dimensional shape. A convex polyhedron that is bounded by six rectangular faces with eight vertices and twelve edges is called a cuboid. A cuboid is also called a rectangular prism. A cuboid with six square faces is called a cube. An example of a cuboid in real life is a rectangular box.
In Maths, we can observe other shapes which are exactly the same as cuboid, they are rectangular cuboid, rectangular box, right rectangular prism, right cuboid, rectangular parallelepiped, and rectangular hexahedron. Let us learn here details of cuboids with examples.
| Table of contents: |
What is a Cuboid?
A cuboid is a three dimensional solid that has 6 faces (rectangular), 8 vertices and 12 edges. A cuboid has three dimensions such as length, width and height. A perfect cuboid is said to be a cuboid that has integer edges.
If we consider Euler’s formula, then the relation between Faces (F), Vertices (V) and Edges (E) of a cuboid satisfies the equation:
F + V = E + 2
6 + 8 = 12 + 2
Cuboid Shape
The cuboid shape is a closed 3d figure that is enclosed by rectangular faces that means plane regions of rectangles. The shape of a cuboid is shown in the below figure.
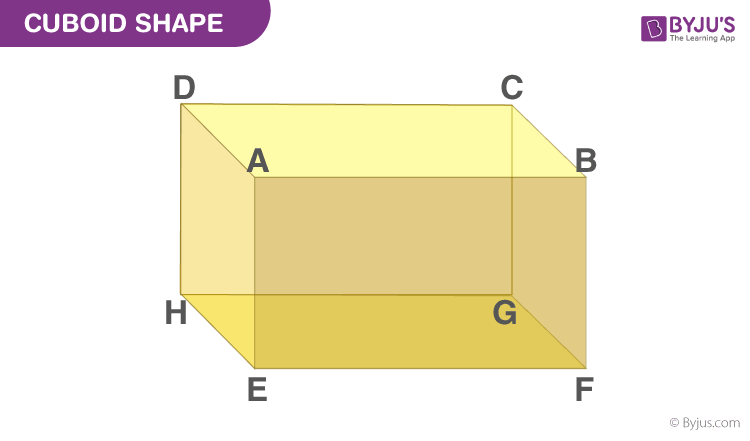
Faces, Edges and Vertices of Cuboid
A cuboid has 6 faces, 8 vertices and 12 edges. All these can be shown using notation as given below:
Faces of Cuboid
A Cuboid is made up of six rectangular faces. In the above-given figure, the six faces are:
- ABFE
- DAEH
- DCGH
- CBFG
- ABCD
- EFGH
The pair of opposite and parallel faces of the given cuboid are:
ABCD and EFGH (top and bottom faces respectively)
ABFE, DCGH, and DAEH, CBFG (opposite and parallel faces which are adjacent to top and bottom faces of the cuboid)
For each face, we can write the remaining faces as their adjacent faces such as the face ABCD is the adjacent face to ABFE, BCGF, CDHG, and ADHE.
Edges of Cuboid
The sides of all the rectangular faces are referred to as the edges of the cuboid. As we know, there are 12 edges for a cuboid. They are AB, AD, AE, HD, HE, HG, GF, GC, FE, FB, EF and CD respectively. Also, the opposite sides of a rectangle are equal. Therefore,
- AB = CD = GH = EF
- AE = DH = BF = CG
- EH = FG = AD = BC
Vertices of Cuboid
The point of intersection of the 3 edges of a cuboid is called the vertex of a cuboid and a cuboid has 8 vertices.
From the given cuboid figure, the 8 vertices are A, B, C, D, E, F, G and H.
Let us have a look at the visualization of faces, edges and vertices of a cuboid.

Properties of Cuboid
- A cuboid has 6 faces, 12 edges and 8 vertices
- The faces of the cuboid are all rectangular in shape
- Opposite edges of cuboid are parallel to each other
- Cuboid has three dimensions: length, width and height
- Angles formed at the vertices of the cuboid are all 90 degrees
Surface Area of Cuboid
The surface area of any three-dimensional shape is the total region covered by all its faces. In the same way, the surface area of a cuboid is the sum of areas of all its six rectangular faces. The surface area of cuboidal box can be divided into two types namely lateral surface area and total surface area. The formulas for these can be derived from the figure given below.

Let l, b and h be the length, breadth and height of a cuboid respectively.
From the figure given above,
- AB = CD = EF = GH = l
- BC = AD = EH = FG = b
- CG = BF = AE = DH = h
Cuboid Lateral Surface Area
Lateral surface area (LSA) of a cuboid is the sum of areas of all faces except the top and bottom faces.
Lateral surface area of the cuboid = Area of face ADHE + Area of face BCGF + Area of face ABFE + Area of face DCGH
= (AD × DH) + (BC × CG) + (AB × BF) + (CD × BC)
= (b × h) + (b × h) + (l × h) + (l × h)
= 2(b × h) + 2(l × h)
= 2h(l + b)
| Lateral Surface Area (LSA) = 2h(l + b) sq.units |
Cuboid Total Surface Area
Total surface area (TSA) of a cuboid is the sum of areas of all its rectangular faces.
Area of face EFGH = Area of Face ABCD = (l × b)
Area of face BFGC = Area of face AEHD = (b × h)
Area of face DHGC = Area of face ABFE = (l × h)
Total surface area of a cuboid = Sum of the areas of all its 6 rectangular faces
= Area of (ABCD + EFGH + BFGC + AEHD + DHGC + ABFE)
= (l × b) + (l × b) + (b × h) + (b × h) + (l × h) + (l × h)
= 2lb + 2bh + 2hl
= 2(lb + bh + hl)
| Total Surface Area (TSA) = 2(lb + bh + hl) sq.units |
Volume of Cuboid
The volume of a solid is equal to the product of the base area and its height. Thus, the volume of cuboid is equal to the product of the base rectangular face and height.
Volume = (Length × Breadth) × Height
= (l × b) × h
= lbh
| Volume (V) = (l × b × h) cubic units |
Diagonal of Cuboid
The length of the diagonal of a cuboid of dimensions l, b and h is given by the formula:
| Diagonal = √(l2 + b2 + h2) units |
This formula is for the length of space diagonals of a cuboid. Whereas the face diagonals of the cuboid are the diagonals drawn by joining the vertices on a face of the cuboid. For each face there are two diagonals, so the total face diagonals that can be drawn in a cuboid are 12 (6 faces x 2).
Perimeter of Cuboid
The perimeter of a cuboid will be the sum of the lengths of all the edges. Thus, from the above figure 2,
- AB = CD = EF = GH = l (length)
- BC = AD = EH = FG = b (breadth)
- CG = BF = AE = DH = h (height)
Perimeter of the cuboid = AB + CD + EF + GH + BC + AD + EH + FG + CG + BF + AE + DH
= (l + l + l + l) + (b + b + b + b) + (h + h + h + h)
= 4l + 4b + 4h
= 4(l + b + h)
| Perimeter (P) = 4(l + b + h) units |
Cuboid Formulas
The table below shows the formulas of a cuboid of length (l), breadth (b) and height (h).
| Measure | Formula |
| Lateral Surface Area (LSA) | 2h(l + b) |
| Total Surface Area (TSA) | 2(lb + bh + hl) |
| Volume | lbh |
| Diagonal | √(l2 + b2 + h2) |
| Perimeter | 4(l + b + h) |
Cuboid Net
The net of a solid shape is the plane obtained by unfolding it across a line. This net will again form the original solid when we fold it. The number of different nets for a cuboid or rectangular cuboid with 3 different lengths is 54.
Click here to learn more about nets of 3d shapes.
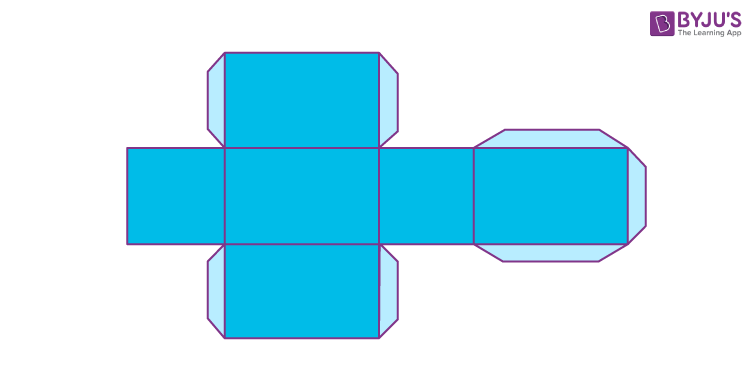
Similarly, the nets of a cuboid can be shown in different ways.
Related Articles
Solved Examples on Cuboid
Below are some example problems solved using the formulas of cuboids.
Example 1:
Find the volume of a cuboid of length 10 cm, breadth 8 cm and height 4 cm.
Solution:
Given,
Length = l = 10 cm
Breadth = b = 8 cm
Height = h = 4 cm
Volume = lbh
= 10 × 8 × 4
= 320 cm3
Example 2:
Calculate the lateral and total surface area of a cuboid of dimensions 12 cm × 7 cm × 5 cm.
Solution:
Given dimensions of a cuboid are 12 cm × 7 cm × 5 cm.
i.e. l = 12 cm, b = 7 cm, h = 5 cm
Lateral surface area (LSA) = 2h(l + b)
= 2 × 5 (12 + 7)
= 10 × 19
= 190 cm2
Total surface area (TSA) = 2(lb + bh + hl)
= 2(12 × 7 + 7 × 5 + 5 × 12)
= 2(84 + 35 + 60)
Practice Questions
Find the total surface area and volume of cuboid whose dimensions are:
- Length = 3 cm, Width = 2 cm and Height = 1.5 cm
- Length = 6 cm, Width = 4 cm and Height = 3 cm
- Length = 7.5 cm, Width = 3.5 cm and Height = 5 cm
Frequently Asked Questions on Cuboid
What is the definition of a cuboid?
How many edges and corners does a cuboid has?
What is the difference between cube and cuboid?
The main difference between the cube and cuboid is their faces, i.e. the cube has six square-shaped faces, whereas the cuboid has six rectangular faces. That means, all the edges of the cube are equal and the edges of a cuboid can be written as 3 groups of equal edges.
What is the cuboid formula?
The formulas of cuboid are:
Lateral surface area (LSA) = 2h(l + b)
Total surface area = TSA = 2(lb + bh + hl)
Volume (V) = lbh
Perimeter (P) = 4(l + b + h)
Diagonal (D) = √(l^2 + b^2 + h^2)
What is the difference between the cuboid and a rectangular prism?
There is no difference between the cuboid and rectangular prism since both will have 6 rectangular faces, 8 vertices and 12 edges. Also, both look the same as a box.
Can a cuboid have a square face?
As we know, a cube is a special kind of cuboid with all its edges equal in length. Hence, a cuboid can have a square face.
How do you find the area of a cuboid?
To find the total surface area of a cuboid, add the areas of all six faces. Suppose l, b and h be the length, breadth and height of a cuboid, then the total surface area will be 2(lb + bh + hl).