Denominator
The meaning of the denominator is the divisor of a fraction. The denominator is the number or integer that is below the horizontal line in a fraction. Whereas the numerator lies above the line in a fraction. A denominator cannot be equal to 0, else it will result in an indefinite value.
Now you may consider, what a fraction is? The fraction is one part when a whole is divided into equal parts. For example, 1/4 is one part out of the four equal parts created from that one whole thing. So here, 1 is the numerator and 4 is the denominator.
In this article, let us discuss the denominator definition, the comparison between the numerator and the denominator, how to find the least common denominator when the problem involves two or more fractions and rationalizing the denominator with more solved examples.
| Table of Contents: |
What is a Denominator?
A denominator is the bottom part of a fraction. When an integer is expressed as a fraction, then there appear two numbers separated by a horizontal line. The denominator is the number that appears at the bottom of the horizontal line, whereas the number above the line is the numerator. The denominator represents the number of parts an object or an item is divided into.
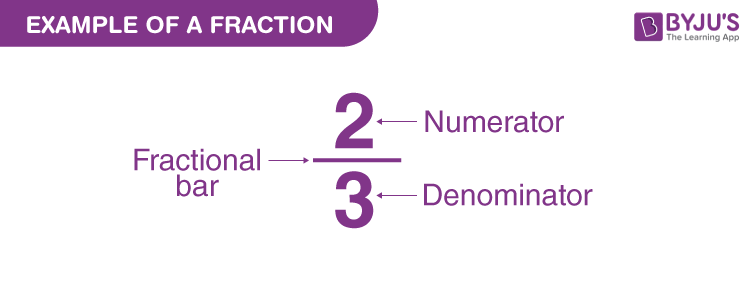
It is not necessary that only numerical values are expressed in the numerator and denominator form, instead, the variables are also expressed in the same form such as x/y, p/q, m/n, etc., where y, q, and n are the denominators respectively.
A fraction consists of two numbers. Symbolically it is represented by two numbers separated by a horizontal line (–) or slash line (/). The number above the line is the numerator, and the number below the line is the denominator. The term denominator is widely used in ratio and proportion concept.
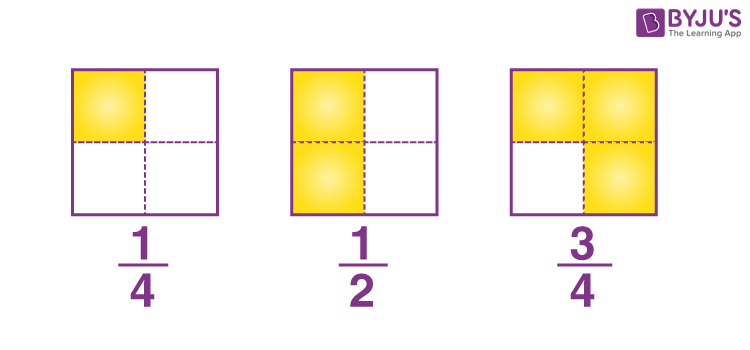
In the above figure, 4, 2, and 4 are the denominators of 1/4, 1/2, and 3/4 respectively.
The denominator value should not be zero. Because, if the value of the denominator is zero, the fraction value should be undefined. For example, 5/0 is a fraction, which is undefined as the denominator value is zero.
Examples of Denominator
As discussed, denominator is the bottom part of a fraction. If x/y is a fraction, then y is the denominator. Some of the examples of the denominator are given below.
| Fractions | Denominator |
| 12/3 | 3 |
| 11/2 | 2 |
| 1/10 | 10 |
| x/2y | 2y |
| m+n/5 | 5 |
| p-q/9 | 9 |
Numerator and Denominator
- The denominator indicates the number of equal parts in which the whole thing has to be divided
- The numerator indicates the number of divisions selected out of the total number of equal parts
- If a/b is a fraction, then a is the numerator and b is the denominator

Example: This would be better explained with the help of an Example.
3/4 is a fraction in which the denominator 4 represents that 4 equal divisions have to be made.
3 parts selected out of 4 equal parts created out from 1 circle can be represented as 3/4.
Diagrammatic representation of ¾ is as follows:

The diagram clearly shows three equal parts taken out when the whole circle is divided into four equal parts.
What is the Common Denominator?
When two or more fractions have the same value in the denominator then they are called common denominators. They are also called like and unlike fractions based on the similarity between the denominators. While performing arithmetic operations such as addition and subtraction, if the denominators of the fractions are common or equal, then it becomes easy to add or subtract them.
But fractions can be multiplied or divided even though the denominators of the fractions are not the same or common. Let us see some examples here;
- 1/2 +3/2 = (1+3)/2 = 4/2 = 2
- 4/7 – 2/7 = (4-2)/7 = 2/7
- 1/2 x 1/3 = (1 x 1)/(2 x 3) = 1/6
- 4/5 ÷ 3/7 = 4/5 x 7/3 = (4 x 7)/(5 x 3) = 28/15
Least Common Denominator (LCD)
The least common denominator of two or more non-zero denominators is the smallest whole number that is divisible by each of the denominators.
How to Find the Least Common Denominator?
1.Multiply both the denominators (when the denominators have no common multiple)
For Example:
There are two fractions as follows:-
⅓ and ⅕
3 x 5 = 15
Multiply both the fractions with the product (15) with the top as well as the bottom:
⅓ x 15/15 = 5/15
⅕ x 15/15 = 3/15
Thus, we have a common denominator in both our fractions.
2. List the multiples of both denominators:
We have two fractions: ⅓ and ⅙
3 = 3, 6, 9, 12, 18, 21, 24, 27, 30.
6 = 6, 12, 18, 24, 30, 36, 42, 48, 60.
The smallest common multiple that can be seen is 6.
Rationalizing the Denominator
The denominator of a fraction needs to be rationalized when it is an irrational number so that further calculations can be made easily on the fraction.
The irrational denominator includes the root numbers.
Example 1. Monomial Denominator
\(\frac{1}{\sqrt{3}}\) has an irrational denominator since it is a cube root of 3.
To remove the radical multiply the numerator and denominator by the \(\sqrt{3}\), we have
\(\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{3}\)
By multiplying the top and bottom with the denominator value, we have created the smallest possible perfect square in the denominator and removed the radical as per our requirement.
Example 2. Binomial Denominator:
When there are two terms in the denominator that make it irrational.
\(\frac{3}{5 + \sqrt{3}}\)
In this case, multiply the numerator and denominator with the conjugate of the denominator.
The conjugate means the same denominator but with the opposite sign.
The conjugate of \(5 + \sqrt{3}\) is \(5 – \sqrt{3}\), where the “+ sign “ is replaced with “- sign”.
To rationalize:
\(\frac{3}{5 + \sqrt{3}} \times \frac{5 – \sqrt{3}}{5 – \sqrt{3}}\)
\(\frac{15 – 3\sqrt {3}}{5^{2} – (\sqrt{3})^{2}} = \frac{15 – 3\sqrt {3}}{22}\)
Related Articles
Solved Examples on Denominator
Q.1: If a cake is divided into four equal parts, then each part is represented by a fraction. What is the denominator of such a fraction?
Solution: The whole cake is represented by 1.
Now if it is divided into four equal parts, then each part will be 1/4th of the whole.
Hence, the denominator of fraction is 4.
Q.2: Rohan brings a pizza, that has six equal pieces. If he ate one piece, then what is the denominator of the remaining part of the pizza?
Solution: The pizza is divided into six equal parts.
Fraction of one piece of pizza is 1/6
Fraction of the remaining piece of pizza is 5/6
Hence, the required denominator is 6.
Practice Questions
Write the denominator part for the following fractions.
- 1/8
- 2/7
- x/z
- (x+1)/x
- 1/(1-x)
Frequently Asked Questions on Denominator
What do you mean by Denominator?
The denominator is the bottom number in a fraction, and we can say that the denominator is the divisor of a fraction. It defines the number of equal parts an item is divided into.
What is the difference between numerator and denominator?
In a fraction, the top number is called the numerator and the bottom number is called the denominator. For example, ⅘ is a fraction. Here, 4 is the numerator and 5 is the denominator. Similarly, the numerator defines how many parts we have and the bottom number represents how many equal parts the object is divided into.
Can a denominator value be zero?
The denominator value of the fraction cannot be negative, because the fraction value becomes undefined if we have zero in the denominator of a fraction.
What is meant by the common denominator?
If two or more fractions contain the same bottom number, it is considered as the common denominator. We can add or subtract fractions directly if the fractions have a common denominator. For instance, ⅔ and 4/3 are the two fractions, and the common denominator is 3.
What does the denominator represent?
In a fraction, the denominator represents how many equal parts the object/item is divided into, whereas the numerator represents how many parts we have.
This was all about denominator and how to rationalize the fraction. Learn more about ratio and proportion, percentage, fractions, etc., by visiting our site BYJU’S.