In analytical geometry, the directional cosines also known as direction cosine of a vector is defined as the cosines of the angles between the three coordinate axes and the vector.  In this section, we will first learn about the position vector of a point and direction cosines and then finding the angle between two lines.

Position Vector

If O is taken as reference origin and A is an arbitrary point in space then the vector \(\overrightarrow{OA}\) is called the position vector of the point.

Position vector simply denotes the position or location of a point in the three-dimensional Cartesian system with respect to a reference origin.

Direction Cosines and Angle Between Two Lines

Let us consider a point P lying in space and if its position vector makes positive angles (anticlockwise direction) of α, β and γ with the positive x,y and z-axis respectively, then these angles are known as direction angles and on taking the cosine of these angles we get direction cosines. Taking direction cosines makes it easy to represent the direction of a vector in terms of angles with respect to the reference.

The coordinates of the point P may also be expressed as the product of the magnitude of the given vector and the cosines of direction on the three axes, i.e.

\(x = l| \vec{r} | \)

\( y = m| \vec{r} | \)

\( z = n| \vec{r} | \)

Where l, m, n represent the direction cosines of the given vector on the axes x, y, z respectively. We can clearly see that lr, mr, nr are in proportion to the direction cosines and these are called the direction ratios and they are denoted by a, b, c.

Let L₁ and L₂ represent two lines having the direction ratios as a₁, b₁, c₁ and a₂, b₂, c₂ respectively such that they are passing through the origin. Let us choose a random point A on line L₁ and B on line L₂. Considering the directed lines OA and OB as shown in the figure given below, let the angle between these lines be θ.

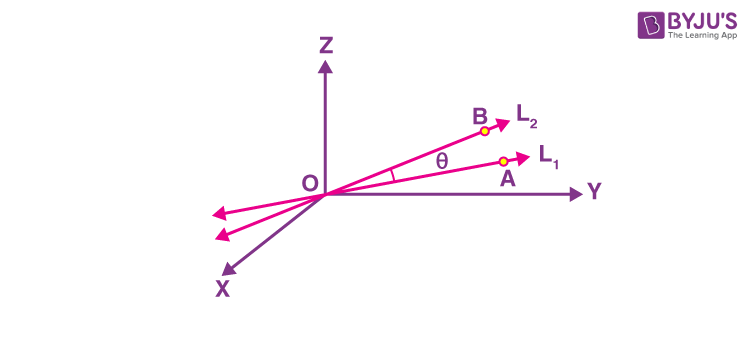
Using the concept of direction cosines and direction ratios, the angle θ between L₁ and L₂ is given by:

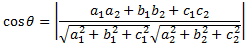
In terms of sin θ = \(\sqrt{(1 – cos^2 θ)}\)

Therefore,

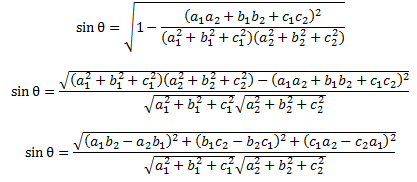
Special Cases

• If L₁ and L₂ having the direction ratios as a₁, b₁, c₁ and a₂, b₂, c₂ respectively are perpendicular to each other, then θ = 90⁰. Therefore, a₁a₂ + b₁b₂ + c₁c₂ = 0

• If L₁ and L₂ having the direction ratios as a₁, b₁, c₁ and a₂, b₂, c₂ respectively are parallel to each other, then θ = 0⁰. Therefore, \(\frac{a_1}{a_2}\) = \(\frac{b_1}{b_2}\) = \(\frac{c_1}{c_2}\)

How to Find the Direction Cosine?

The direction cosine of the vector can be determined by dividing the corresponding coordinate of a vector by the vector length. The unit vector coordinate is equal to the direction cosine. One such property of the direction cosine is that the addition of the squares of the direction cosines is equivalent to one.

We know that the direction cosine is the cosine of the angle subtended by the line with the three coordinate axes, such as x-axis, y-axis and z-axis respectively. If the angles subtended by these three axes are α, β, and γ, then the direction cosines are cos α, cos β, cos γ respectively. The direction cosines are also represented by l, m and n. Thus, the direction cosine of a vector \(\vec{A} = a\hat{i}+b\hat{j}+c\hat{k}\) is given as:

\(cos\alpha = l = \frac{a}{\sqrt{(a)^{2}+(b)^{2}+(c)^{2}}}\)

\(cos\beta = m = \frac{b}{\sqrt{(a)^{2}+(b)^{2}+(c)^{2}}}\)

\(cos\gamma = n = \frac{c}{\sqrt{(a)^{2}+(b)^{2}+(c)^{2}}}\)

Direction Cosines Examples

Example 1: 

Determine the direction cosine of a line joining the point (-4, 2, 3) with the origin.

Solution:

Given that, the line joins the origin (0, 0, 0) and the point (-4, 2, 3). Hence, the direction ratios are -4, 2, 3.

Also, the magnitude of a line = √[(-4)²+(2)²+(3)²]

= √(16+4+9) = √29.

Therefore, the direction cosines are ((-4/√29), (2/√29), (3/√29)).

Example 2: 

Find the direction cosine of a vector joining the points A(1, 2, -3) and B(-1, -2, 1), directed from A to B.

Solution:

Given that, A(1, 2, -3) and B(-1, -2, 1)

\(\overrightarrow{AB} = (-1-1)\hat{i}+(-2-2)\hat{j}+(1-(-3))\hat{k}\)

\(\overrightarrow{AB} = -2\hat{i}-4\hat{j}+4\hat{k}\)

Hence, the direction ratios are -2, -4, 4.

Magnitude = √[(-2)²+(-4)²+(4)²]

= √(4+16+16) = √36 = 6.

Thus, the direction cosines are (-2/6, -4/6, 4/6), which is also equal to (-⅓, -⅔, ⅔)

Example 3: 

Determine the direction cosine of the vector \(1\hat{i}+2\hat{j}+3\hat{k}\)

Solution:

Given vector: \(1\hat{i}+2\hat{j}+3\hat{k}\)

Let \(\vec{a}= 1\hat{i}+2\hat{j}+3\hat{k}\)

Thus, the direction ratios are 1, 2, 3.

Magnitude of \(\vec{a}\) = √[(1)²+(2)²+(3)²]

= √(1+4+9) = √14.

Therefore, the direction cosines are ((1/√14), (2/√14), (3/√14))

Stay tuned with BYJU’S – The Learning App and download the app to learn all Maths-related concepts easily by exploring more videos.