Distance between two points can be evaluated if we know the coordinates of the two points in the XY plane. If P(x₁, y₁) and Q(x₂, y₂) are the two points in a plane, then the distance between P and Q can be evaluated using the distance formula, such as:

\(PQ = \sqrt{(x_{2}- x_{1})^{2}+ (y_{2}- y_{1})^{2}}\)

The difference between the x-axis coordinates gives the horizontal distance and the difference between the y-axis coordinates gives the vertical distance.

Using this formula, we can find the distance between any two points in geometry and in real life as well. For example, finding the distance between two cities, or any two points on earth, on a map. Before learning how to find the distance between two points in coordinate geometry, let’s understand what are the coordinates of a given point and how to represent it.

What are the Coordinates of a point?

In Euclidean geometry, we came across the points, that was positioned in the plane. These points are defined by their coordinates along the x-axis and y-axis. Therefore, the coordinates of a point are a pair of values that exactly define the location of that point in the coordinate plane.

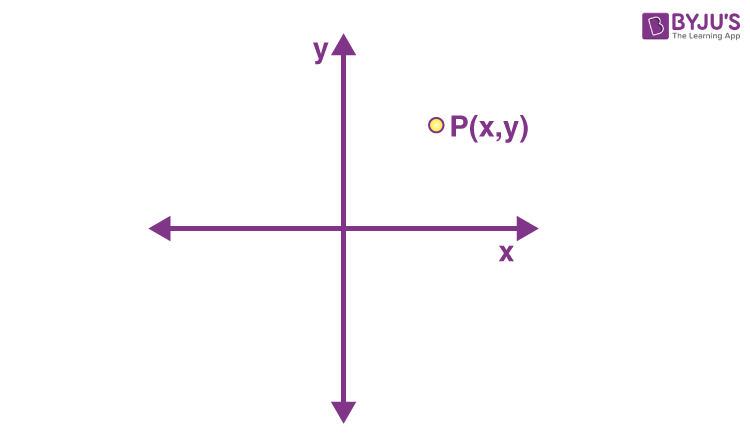
In the above figure, the coordinates of point P in the two-dimensional plane is (x, y). It means that the point, P is x units away from the y-axis and y units away from the x-axis.

Coordinates of a point on the x-axis are of the form (a, 0), where a is the distance of the point from the origin, and on the y-axis is of the form (0, a), where a is the distance of the point from the origin.

Distance Between Two Points – Using Pythagoras Theorem

Consider the following situation.

A boy walks towards the north 30 meters and took a turn to the east and walked for 40 meters more. How do we calculate the shortest distance between the initial place and final place?

A pictorial representation of the above situation is:

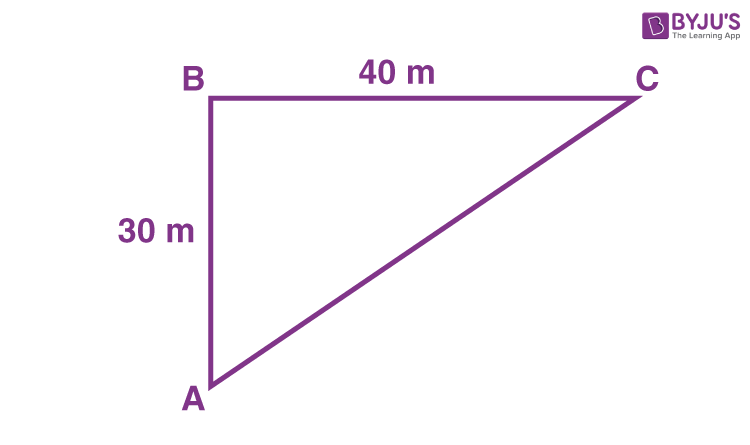
The initial point is A and the final point is C. The distance between points A, B is 30 m and between points B, C is 40 m.

The shortest distance between points A and C is AC. This distance is calculated using the Pythagoras theorem as follows.

AC² = AB² + BC²

\( AC \) = \( \sqrt{30^2~+~40^2}\) = 50 m

Hence, we got the distance between the start point and the endpoint. In the same way, the distance between two points in a coordinate plane is also calculated using the Pythagorean theorem or right-angle triangle theorem.

Before going to derive the formula for distance between two points in a coordinate plane, let us understand what are the coordinate points and how to locate them in the Cartesian plane.

Distance Formula for Two points

The distance between two points (x₁, y₁) and (x₂, y₂) can be derived using the Pythagoras theorem as shown in the figure given below:

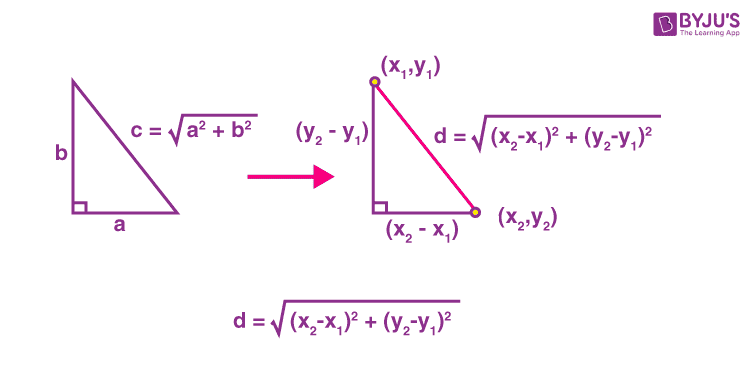
How to Derive Distance Between Two Points Formula?

As we already have learned the distance formula for two points in a plane is given by:

\(PQ = \sqrt{(x_{2}- x_{1})^{2}+ (y_{2}- y_{1})^{2}}\)

Where P and Q are two separate points

Let us see, how this formula came.

Proof:

Suppose we have two points P(x₁, y₁)  and Q(x₂, y₂) in the coordinate plane. Let us represent these points in the figure.

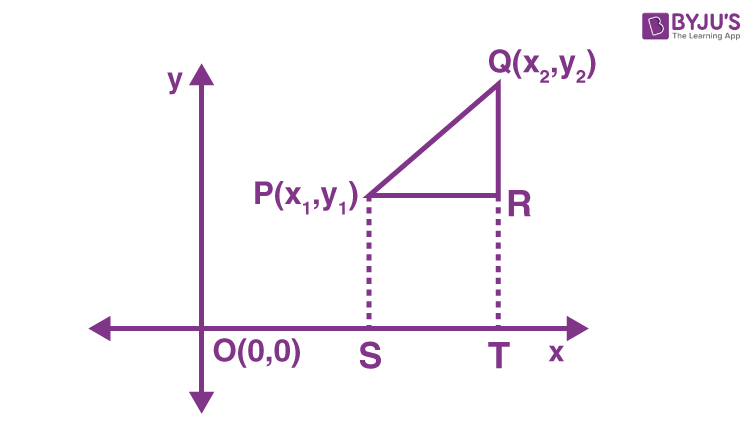
Note that we have taken our points P and Q in the first quadrant itself. What if the points are in other quadrants? As you shall observe in the following discussion, the final formula still remains the same, irrespective of which quadrant P and Q lie in.

PS, QT are perpendicular to the x-axis and PR is parallel to the x-axis.

Distance between the points P and Q is calculated as follows:

S and T are the points on the x-axis which are endpoints of two parallel line segments PS and QT respectively.

⇒ PR = ST

Coordinates of S and T are (x₁, 0) and  (x₂, 0) respectively.

OS =  x₁ and OT = x₂

ST = OT – OS = x₂ – x₁ = PR

Similarly,

PS =  RT

QR = QT – RT = QT – PS = y₂ – y₁

By Pythagoras theorem,

PQ² = PR² + QR²

PQ = √[(x₂– x₁)²+ (y₂– y₁)²]

Therefore,

Distance between two points (x₁,y₁) and (x₂,y₂) is given by:

\(PQ = \sqrt{(x_{2}- x_{1})^{2}+ (y_{2}- y_{1})^{2}}\)

It is known as distance formula.

Observe that (x₂– x₁)²  is the square of the difference in x – coordinates of P and Q and is always positive. The same can be said about (y₂– y₁)² as well. Use this point and try to see for yourself why the formula remains the same for any coordinates of P and Q, in any quadrant.

Distance between a point from the origin

What will be the distance from the origin to a point in a plane? Suppose a point P(x, y) in the xy – plane as shown in the figure below:

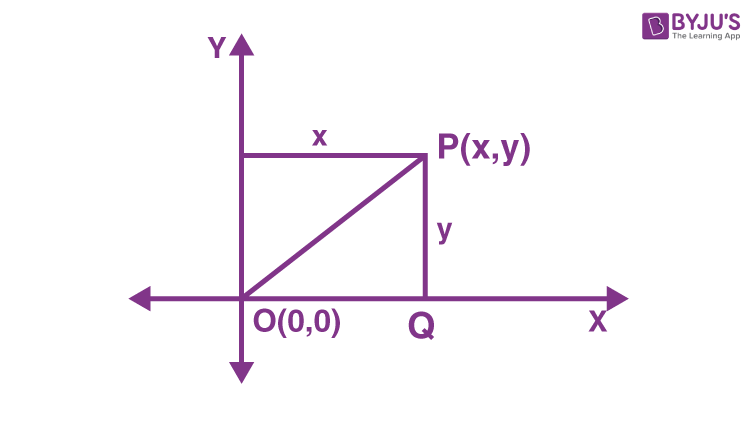
Let us calculate the distance between point P and the origin. P is x units away from y-axis and y units away from the x-axis.

By Pythagoras theorem,

OP² = x² + y²

\( OP \) = \( \sqrt{x^2~+~y^2} \)

Therefore distance between any point (x, y) in xy-plane and the origin (0, 0) is \( \sqrt{x^2~+~y^2} \).

Also, read:

Solved Examples

Example 1: Find the value of a, if the distance between the points P(3, -6) and Q(-3, a) is 10 units.

Solution:

Let the given points be:

P(3, -6) = (x₁, y₁)

Q(-3, a) = (x₂, y₂)

Using distance formula,

Distance between the points P(3, -6) and Q(-3, a) is:

[(-3 – 3)² + (a + 6)²] = 10 units (given)

Squaring on both sides of the equation,

(-6)² + (a + 6)² = 100

(a + 6)² = 100 – 36 = 64 

Taking root on both the sides, we get;

a + 6 = ±8

Case I: Considering +8,

a + 6 = 8 ,

a = 8 – 6 = 2

Case II: Considering -8

a + 6 = -8

a = -8 – 6

a = -14

Therefore, the coordinates are either P(3, -6) and Q(-3, 2) or P(3, -6) and Q(-3, -14).

Example 2: Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).

Solution: Let P(x, y) be the point which is equidistant from the points A(7, 1) and B(3, 5).

Given,

AP = BP

⇒ AP² = BP²
(x – 7)² + (y – 1)² = (x – 3)² + (y – 5)²  (by distance formula)
x² – 14x + 49 + y² – 2y + 1 = x² – 6x + 9 + y² – 10y + 25

-14x + 50 – 2y + 6x + 10y – 34 = 0

-8x + 8y = -16
x – y = 2
This is the required relation between x and y.

Example 3: Find a point on the y-axis which is equidistant from points A(6, 5) and B(– 4, 3).

Solution: We know that a point on the y-axis is of the form (0, y). So, let the point P(0, y) be equidistant from A and B. Then:

AP = BP

⇒ AP² = BP²

(6 – 0)² + (5 – y)² = (– 4 – 0)² + (3 – y)²
36 + 25 + y²– 10y = 16 + 9 + y² – 6y

61 – 10y = 25 – 6y

⇒ 10y – 6y = 61 – 25
⇒ 4y = 36
⇒ y = 9

So, the required point is (0, 9).

Verification:

AP = √[(6 – 0)² + (5 – 9)²]

= √(36+16)

= √52

BP =  √[(-4-0)²+(3-9)²]

=√(16+36)

=√52

Hence, we conclude that the point (0, 9) is equidistant from the given two points.

Distance Between Two Points in 3D

The distance between two points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) in a three-dimensional plane is given by the formula:

\(AB = \sqrt{(x_{2}- x_{1})^{2}+ (y_{2}- y_{1})^{2}+(z_{2}-z_{1})^{2}}\)

Here,

(x₂– x₁)²  is the square of the difference in x – coordinates of A and B and is always positive.

Similarly, (y₂– y₁)² and (z₂– z₁)² are equal to the square of the difference between the corresponding y and z– coordinates of A and B.

Practice Problems

1. What is the distance between two points (-4, 7) and (0, 8)?
2. If the distance between the points (4, p) and (1, 0) is 5, then find the value of p.
3. What type of a quadrilateral do the points A (2, –2), B (7, 3), C (11, –1) and D (6, –6) taken in that order, form?
4. Find a point that is equidistant from points A(–5, 4) and B(–1, 6)? How many such points are there?

To learn more about coordinate geometry and related topics and to watch interactive videos, download BYJU’S – The Learning App.