The physical quantities which have magnitude, as well as directly attached to them, are known as vectors. Position vectors simply denote the position or location of a point in the three dimensional Cartesian systems with respect to a reference origin. In the upcoming discussion, we shall study about vectors and the Cartesian equation of a plane in three dimensions.

In the previous section we have already discussed that to a given vector there lie infinite planes which are perpendicular to it. But for a particular point there exist one and only one unique plane which is perpendicular to it passing through the given point. The vector equation of a plane in this case is given as

\((\vec{r} – \vec{a}) . \vec{N} = 0\)

Here,  \(\vec{r} \)  and  \(\vec{a} \) represent the position vectors.

The Cartesian equation of such a plane is represented by:

\(A(x-{x}_{1}) + B (y- {y}_{1}) + C (z -{z}_{1}) = 0 \)

Here, A, B, and C are the direction ratios.

Let us now discuss the equation of a plane passing through three points which are non-collinear.

Equation of a Plane Passing through Three Non Collinear Points

Let us consider three non collinear points P, Q, R lying on a plane such that their position vectors are given by \(\vec{a} \) , \(\vec{b} \)   and \(\vec{c} \)  as shown in the figure given below.

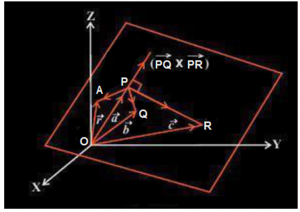
The vectors  \(\vec{PQ} \) and  \(\vec{PR} \) lie in the same plane. The vector lying perpendicular to plane containing the points P, Q and R is given by   \(\vec{PQ} \) × \(\vec{PR} \) . If  is the position vector of any point A lying in the plane containing P, Q, R then using the vector equation of a plane as mentioned above, the equation of the plane passing through P and perpendicular to the vector \(\vec{PQ} \) × \(\vec{PR} \)  is given by

(\(\vec{r} \) – \(\vec{a} \)). (\(\vec{PQ} \) × \(\vec{PR}) = 0\)

Also, from the above figure,  and . Substituting these values in the above equation, we have

\((\vec{r} – \vec{a}).[(\vec{b}- \vec{a}) × (\vec{c}- \vec{a})] = 0 \)

This represents the equation of a plane in vector form passing through three points which are non- collinear.

To convert this equation in Cartesian system, let us assume that the coordinates of the point P, Q and R are given as (x₁, y₁, z₁), (x₂, y₂, z₂) and (x₃, y₃, z₃) respectively. Also let the coordinates of point A be  x, y and z.

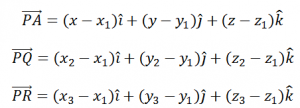
Substituting these values in the equation of a plane in Cartesian form passing through three non-collinear points, we have

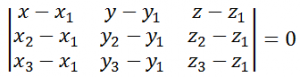
This is the equation of a plane in Cartesian form passing through three points which are non- collinear.

Stay tuned with BYJU’S – The Learning App and download the app to learn all Maths-related concepts quickly by exploring more videos.