Equation of a Line
The standard forms of the equation of a line are:
- Slope-intercept form
- Intercept form
- Normal form
Let us learn all the straight lines formulas along with the general equation of a line and different forms to find the equation of a straight line in detail here.
General Equation of a Line
The general equation of a line in two variables of the first degree is represented as
Ax + By +C = 0,
A, B ≠ 0 where A, B and C are constants which belong to real numbers.
When we represent the equation geometrically, we always get a straight line.
Below is a representation of straight-line formulas in different forms:
Slope-intercept Form
We know that the equation of a straight line in slope-intercept form is given as:
| y = mx + c |
Where m indicates the slope of the line and c is the y-intercept
When B ≠ 0 then, the standard equation of first degree Ax + By + C = 0 can be rewritten in slope-intercept form as:
y = (− A/B) x − (C/B)
Thus, m= –A/B and c = –C/B .
Intercept Form
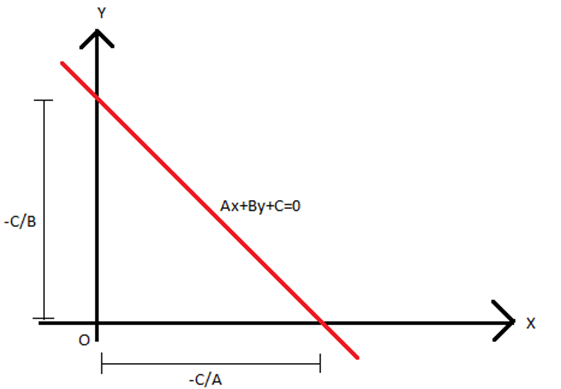
The intercept of a line is the point through which the line crosses the x-axis or y-axis. Suppose a line cuts the x-axis and y-axis at (a, 0) and (0, b), respectively. Then, the equation of a line making intercepts equal to a and b on the x-axis and the y-axis respectively is given by:
x/a + y/b = 1
Now in case of the general form of the equation of the straight line, i.e. Ax+By+C = 0, if C ≠ 0, then Ax + By + C = 0 can be written as;
x/(-C/A) + y/(-C/B) = 1
where a = -C/A and b = – C/B
Normal Form
The equation of the line whose length of the perpendicular from the origin is p and the angle made by the perpendicular with the positive x-axis is given by α is given by:
x cos α+y sin α = p
This is known as the normal form of the line.
In case of the general form of the line Ax + By + C = 0 can be represented in normal form as:
A cos α = B sin α = – p
From this we can say that cos α = -p/A and sin α = -p/B.
Also it can be inferred that,
cos2α + sin2α = (p/A)2 + (p/B)2
1 = p2 (A2 + B2/A2 .B2)
\(\Rightarrow p = \left (\frac{AB}{\sqrt {A^{2} + B^{2}}} \right )\)
From the general equation of a straight line Ax + By + C = 0, we can conclude the following:
- The slope is given by -A/B, given that B ≠ 0.
- The x-intercept is given by -C/A and the y-intercept is given by -C/B.
- It can be seen from the above discussion that:
\(p = \pm\left (\frac{AB}{\sqrt {A^{2} + B^{2}}} \right )\) , \(\cos \alpha = \pm \left (\frac{B}{\sqrt {A^{2} + B^{2}}} \right )\) , \(\sin \alpha = \pm \left (\frac{A}{\sqrt {A^{2} + B^{2}}} \right )\) - If two points (x1, y1) and(x2, y2)are said to lie on the same side of the line Ax + By + C = 0, then the expressions Ax1+ By1 + C and Ax2 + By2 + C will have the same sign or else these points would lie on the opposite sides of the line.
Straight Line Formulas
Let us accumulate the straight line formulas we have discussed so far:
| Slope (m) of a non-vertical line passing through the points (x1 , y1 ) and (x2, y2 ) | m=(y2-y1)/(x2-x1), x1≠x2 |
| Equation of a horizontal line | y = a or y=-a |
| Equation of a vertical line | x=b or x=-b |
| Equation of the line passing through the points (x1 , y1 ) and (x2, y2 ) | y-y1= [(y2-y1)/(x2-x1)]×(x-x1) |
| Equation of line with slope m and intercept c | y = mx+c |
| Equation of line with slope m makes x-intercept d. | y = m (x – d). |
| Intercept form of the equation of a line | (x/a)+(y/b)=1 |
| The normal form of the equation of a line | x cos α+y sin α = p |
Example of Straight Lines
To understand this concept better go through the below examples:
(1) The equation of a line is given by, 2x – 6y +3 = 0. Find the slope and both the intercepts.
Solution:
The given equation 2x – 6y + 3 = 0 can be represented in slope-intercept form as:
y = x/3 + 1/2
Comparing it with y = mx + c,
Slope of the line, m = 1/3
Also, the above equation can be re-framed in intercept form as;
x/a + y/b = 1
2x – 6y = -3
x/(-3/2) – y/(-1/2) = 1
Thus, x-intercept is given as a = -3/2 and y-intercept as b = 1/2.
(2) The equation of a line is given by, 13x – y + 12 = 0. Find the slope and both the intercepts.
Solution: The given equation 13x – y + 12 = 0 can be represented in slope-intercept form as:
y = 13x + 12
Comparing it with y = mx + c,
Slope of the line, m = 13
Also, the above equation can be re-framed in intercept form as;
x/a + y/b = 1
13x – y = -12
x/(-12/13) + y/12 = 0
Thus, x-intercept is given as a = -12/13 and y-intercept as b = 12.
To learn all the concepts in Math in a more engaging way, register at BYJU’S. Also, watch interesting videos on various maths topics by downloading BYJU’S– The Learning App from Google Play Store or the app store.