Square root by long division method: Any number can be expressed as a product of prime numbers. This method of representation of a number in terms of the product of prime numbers is termed as the prime factorization method. It is the easiest method known for the manual calculation of the square root of a number. But this method becomes tedious and tiresome when the number involved is large. Therefore, to find the square root of large numbers we use the long division method.

Also, to find the square roots of imperfect squares such as 2,3,5,6,8,etc., we can use a long division method avoiding the use of calculators. As we know that division method is used to find the square root of a number, prime factors of a given number, lcm and hcf of given numbers. In this article, you will learn how to solve square root problems using a division method. 

The division method of square root is a very familiar and easy method available to get the accurate roots of numbers. In this method, we can see 5 major steps such as divide, multiply, subtract, bring down and repeat.

Square root of a number by long division method

Let us understand the long division method with the help of an example.

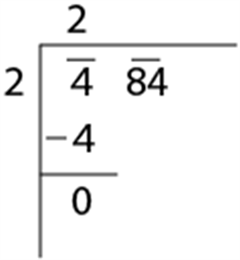
1. Taking 484 as the number whose square root is to be evaluated. Place a bar over the pair of numbers starting from the unit place or Right-hand side of the number. In case, if we have the total number of digits as odd number, the leftmost digit will also have a bar, \( \overline{4}\)  \( \overline{8 4} \).
2. Take the largest number as the divisor whose square is less than or equal to the number on the extreme left of the number. The digit on the extreme left is the dividend. Divide and write the quotient. Here the quotient is 2 and the remainder is 0.
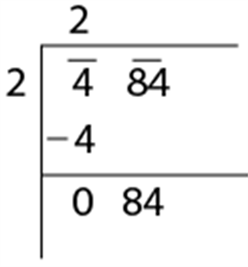
3. Next, we then bring down the number, which is under the bar, to the right side of the remainder. Here, in this case, we bring down 84. Now, 84 is our new dividend.
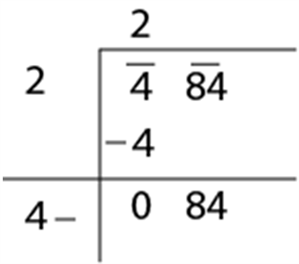
4. Now double the value of the quotient and enter it with blank space on the right side.
   
5. Next, we have to select the largest digit for the unit place of the divisor (4_) such that the new number, when multiplied by the new digit at unit’s place, is equal to or less than the dividend (84).

In this case,  42 × 2 = 84. So the new digit is 2.

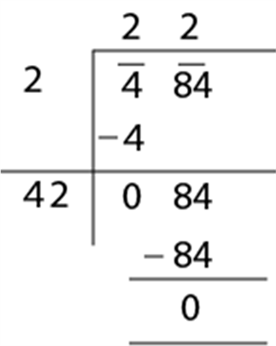
6. The remainder is 0, and we have no number left for division, therefore,

           \( \sqrt{484} \) = 22

More Square Roots

Check here to find the square root of more numbers such as 2,3,5,7,8, etc. using a long division method.

• Square Root Of 2
• Square Root Of 3
• Square Root Of 5
• Square Root Of 6
• Square Root of 7
• Square Root Of 8
• Square Root of 10
• Square Root of 11
• Square Root Of 12

To learn more about other topics download BYJU’S – The Learning App and watch interactive videos. Also, take free tests to practice for exams.