Important 2 Marks Questions for CBSE 8 Maths
Class 8th CBSE is a very important stage in the development of the fundamentals of a student. The basics of Maths and Science help students understand complex topics that will come in 9th standard. Most of the subjects in class 8 are vast, where some of them require memorization and skill. One such is the subject of Mathematics, which seems to be a nightmare for students and requires a lot of practice to boost confidence. So we at BYJU’S provide Class 8 with important 2 marks questions and solutions, which can be beneficial for students in their examination.
Students preparing for CBSE Class 8 Maths Examination are advised to solve the given questions and verify their solutions. Additional questions are also provided here so that students can improve their problem-solving skills and prepare for their exams by solving a variety of problems in mathematics.
Important 2 Marks Questions and Solutions for Class 8 Maths CBSE Board are as follows-
Question 1- Select those which can be written as a rational number with denominator 4 in their lowest form:
\(\frac{7}{8},\frac{64}{16},\frac{36}{-12},\frac{-16}{17},\frac{5}{-4},\frac{140}{28}\)
Solution:
Let us write the given rational numbers with denominator 4 (if possible) are:
7/8 = 7/8
64/16 = 16/4
36/-12 = -12/4
-16/17 = -16/17
5/-4 = -5/4
140/28 = 20/4
Therefore, the rational numbers with denominator 4 in their lowest form are 64/16, 36/-12, 5/-4 and 140/28.
Question 2- Using suitable rearrangement and find the sum:
a) \(\frac{4}{7}+\left (\frac{-4}{9} \right )+\frac{3}{7}+\left (\frac{-13}{9} \right )\)
b) -5 + \(\frac{7}{10}+\frac{3}{7}+(-3)+\frac{5}{14}+\frac{-4}{5}\)
Solution:
(a) (4/7) + (-4/9) + (3/7) + (-13/9)
= (4/7) + (3/7) – (4/9) – (13/9)
= [(4 + 3)/7] – [(4 + 13)/9]
= (7/7) – (17/9)
= 1 – (17/9)
= (9 – 17)/9
= -8/9
Therefore, (4/7) + (-4/9) + (3/7) + (-13/9) = -8/9.
(b) -5 + (7/10) + (3/7) + (-3) + (5/45) + (-4/5)
= -5 + (-3) + (7/10) + (-4/5) + (3/7) + (5/14)
= -(5 + 3) + [(7-8)/10] + [(6 + 5)/14] {since LCM of 5 and 10 is 10, LCM of 7 and 14 is 14}
= -8 – (1/10) + (11/14)
= (-560 – 7 + 55)/70 {since the LCM of 1, 10 and 14 is equal to 70}
= -512/70
= -256/35
Therefore, -5 + (7/10) + (3/7) + (-3) + (5/45) + (-4/5) = -256/35.
Question 3- Following are the number of members in 25 families of a village:
6, 8, 7, 7, 6, 5, 3, 2, 5, 4, 3, 3, 2, 5, 6, 8, 7, 7, 4, 3, 6, 6, 6, 7, 5.
Make a frequency distribution table for the data using class intervals 0 – 2, 2 – 4, etc.
Solution:
Given,
6, 8, 7, 7, 6, 5, 3, 2, 5, 4, 3, 3, 2, 5, 6, 8, 7, 7, 4, 3, 6, 6, 6, 7, 5.
Let us arrange these numbers in the ascending order.
2, 2, 3, 3, 3, 3, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8
The frequency distribution table for the given data using class intervals 0 – 2, 2 – 4, etc., is given below:
| Class intervals | Frequency |
| 0 – 2 | 0 |
| 2 – 4 | 6 |
| 4 – 6 | 6 |
| 6 – 8 | 11 |
| 8 – 10 | 2 |
| Total | 25 |
Question 4- 13 and 31 is a strange pair of numbers such that their squares 169 and 961 are also mirror images of each other. Can you find two other such pairs?
Solution:
From the given,
(13)2 = 169
(31)2 = 961
Similarly, we can write some other numbers.
Pair 1: 12 and 21
(12)2 = 12 × 12 = 144
(21)2 = 21 × 21 = 441
Pair 2: 102 and 201
(102)2 = 102 × 102 = 10404
(201)2 = 201 × 201 = 40401
Question 5- Three numbers are in the ratio 2 : 3 : 4 . the sum of their cubes is 0.334125. Find the numbers.
Solution:
Given,
The ratio of three numbers is 2 : 3 : 4.
Let 2x, 3x and 4x be the three numbers.
According to the given,
(2x)3 + (3x)3 + (4x)3 = 0.334125
8x3 + 27x3 + 64x3 = 0.334125
99x3 = 0.334125
x3 = 334125/(1000000 × 99)
= 3375/1000000
x = ∛(3375/1000000)
= ∛[(15 × 15 × 15)/(100 × 100 × 100)]
= 15/100
= 0.15
2x = 2(0.15) = 0.3
3x = 3(0.15) = 0.45
4x = 4(0.15) = 0.6
Therefore, the three numbers are 0.3, 0.45 and 0.6.
Question 6- A steamer goes downstream and covers the distance between two ports in 5 hours while it covers the same distance upstream in 6 hours. If the speed of the stream is 1 km/hr, find the speed of the steamer in still water.
Solution:
Given,
Speed of the stream = 1 km/hr
Let speed of the streamer be x km/hr
So, the downstream speed = (x + 1) km/hr
Upstream speed = (x – 1) km/hr
According to the given,
5(x + 1) = 6(x – 1)
5x + 5 = 6x – 6
6x – 5x = 5 + 6
x = 11
Therefore, the speed of streamer in still water = 11 km/hr
Distance between two ports = (11 + 1) × 5 = 12 × 5 = 60 km
Question 7- Sum of the digits of a two-digit number is 11. The given number is less than the number obtained by interchanging the digits by 9. Find the number.
Solution:
Let xy be the two-digit number.
So, x + y = 11….(i)
According to the given,
(10y + x) – (10x + y) = 9
10y + x – 10x – y = 9
-9x + 9y = 9
9(-x + y) = 9
-x + y = 1….(ii)
Adding equations (i) and (ii),
x + y – x + y = 11 + 1
2y = 12
y = 6
Substituting y = 10 in (i),
x = 11 – 6 = 5
Therefore, the number is 56.
Question 8- A playground in the town is in the form of a kite. The perimeter is 106 meters. If one of its sides is 23 meters, what are the lengths of the other three sides?
Solution:
Let ABCD be the playground in the form of a kite such that AB = AD and BC = CD.
Given, One of the the kite, say AB = 23 m
Perimeter = 106 m
AB + BC + CD + DA = 106
2AB + 2BC = 106 {since AB = AD and BC = CD}
2(AB + BC) = 106
23 + BC = 53
BC = 30 m
Therefore, the lengths of the other three sides are 30 m, 23, and 30 m, respectively.
Question 9- Factorize the following:
a) \(x^{2}\) + 15x + 26
b) \(x^{2}\) = 17x +60
Solution:
(a) x2 + 15x + 26
Let us split the middle term.
= x2 + 2x + 13x + 26
= x(x + 2) + 13(x + 2)
= (x + 13)(x + 2)
Therefore, the factorization of x2 + 15x + 26 is (x + 13)(x + 2).
(b) x2 – 17x + 60
Let us split the middle term.
= x2 – 12x – 5x + 60
= x(x – 12) – 5(x – 12)
= (x – 5)(x – 12)
Therefore, the factorization of x2 – 17x + 60 is (x – 5)(x – 12).
Question 10- Archana bought medicines from a medical store as prescribed by her doctor for Rs. 36.40 including 4% VAT. Find the price before VAT was added.
Solution:
Given,
Price of the medicine including VAT = Rs. 36.40
VAT = 4%
Actual price = Price including VAT – VAT
= Rs. 36.40 – 4% of Rs. 36.40
= Rs. 36.40 – (4/100) × Rs. 36.40
= Rs. 36.40 – Rs. 1.456
= Rs. 34.944
Therefore, the price of medicines before VAT is Rs. 34.944.
CBSE Class 8 Maths 2 Marks Important Questions for Practice
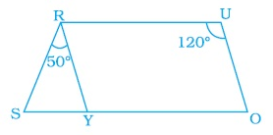
Q.1: In the parallelogram given below YOUR, \(\angle RUO=120^{\circ}\) and OY is extended to point S such that \(\angle SRY=50^{\circ}\) .Find \(\angle YSR\)
Q.2: A polyhedron has 20 faces and 12 vertices. Find the edges of the polyhedron.
Q.3: In a town, an ice cream has displayed ice cream sculpture of height 360 cm. The ice cream parlour claims that these ice creams and the sculpture are in the ratio 1 : 30. What is the height of the ice creams served?
Q.4: The area of the square is given by \(4x^{2}\) + 12xy + \(9y^{2}\) . Find the side of the square.
Q.5: Express as power of a rational number with negative exponent.
- a) \(\left ( \left ( \frac{-3}{2} \right )^{-2} \right )^{-3}\)
- b) \((2^{5}\div2^{8}) \times 2^{-7}\)
Q.6: By what number should \(\left ( \frac{-3}{2} \right )^{-3}\) be divided so that the quotient may be \(\left ( \frac{4}{27} \right )^{-2}\) ?
Q.7: Jyothi bought a product for Rs. 3,155 including 4.5% sales tax. Find the price before tax was added.
Q.8: The variable x varies directly as y and x = 80 when y is 160. What is y when x is 64?
Q.9: Gopi types 108 words in 6 minutes. How many words would she type in half an hour?
Q.10: The walls and ceiling of a room are to be plastered. The length, breadth and height of the room are 4.5 m, 3 m and 350 cm respectively. Find the cost of plastering at the rate of Rs. 8 per \(m^{2}\) .
For more important questions for class 8 download BYJU’S-The learning App.