Introduction To Trigonometry Class 10 Notes

Home → Introduction To Trigonometry Class 10 Notes

CBSE Class 10 Maths Trigonometry Notes:-Download PDF Here

Class 10 Maths Chapter 8 Introduction to Trigonometry Notes

The notes for trigonometry class 10 Maths is provided here. Get the complete concept on trigonometry which is covered in Class 10 Maths. Also, get the various trigonometric ratios for specific angles, the relationship between trigonometric functions, trigonometry tables, various identities given here.

Students can refer to the short notes and MCQ questions along with separate solution pdf of this chapter for quick revision from the links below:

Introduction to Trigonometry Short Notes
Introduction to Trigonometry MCQ Practice Questions
Introduction to Trigonometry MCQ Practice Solutions

Trigonometric Ratios

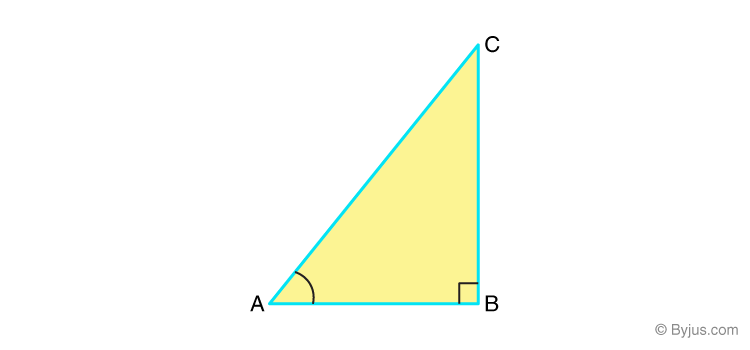
Opposite & Adjacent Sides in a Right Angled Triangle

In the $Δ A B C$ right-angled at B, BC is the side opposite to $∠ A,$ AC is the hypotenuse and AB is the side adjacent to $∠ A .$

Trigonometric Ratios

For the right $Δ A B C$ , right-angled at $∠ B$ , the trigonometric ratios of the $∠ A$ are as follows:

sin A=opposite side/hypotenuse=BC/AC
cos A=adjacent side/hypotenuse=AB/AC
tan A=opposite side/adjacent side=BC/AB
cosec A=hypotenuse/opposite side=AC/BC
sec A=hypotenuse/adjacent side=AC/AB
cot A=adjacent side/opposite side=AB/BC

To know more about Trigonometric Ratios, visit here.

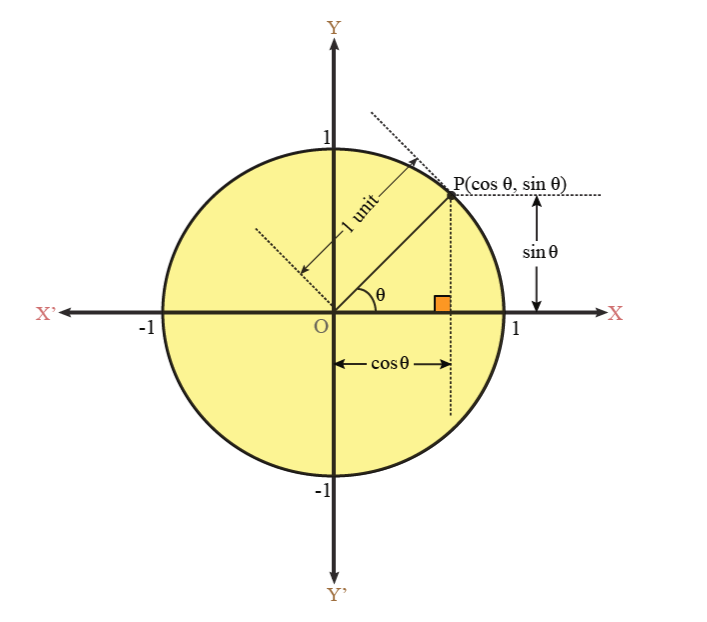
Visualization of Trigonometric Ratios Using a Unit Circle

Draw a circle of the unit radius with the origin as the centre. Consider a line segment OP joining a point P on the circle to the centre which makes an angle $θ$ with the x-axis. Draw a perpendicular from P to the x-axis to cut it at Q.

sinθ=PQ/OP=PQ/1=PQ
cosθ=OQ/OP=OQ/1=OQ
tanθ=PQ/OQ=sinθ/cosθ
cosecθ=OP/PQ=1/PQ
secθ=OP/OQ=1/OQ
cotθ=OQ/PQ=cosθ/sinθ

Visualisation of Trigonometric Ratios Using a Unit Circle

Relation between Trigonometric Ratios

cosec θ =1/sin θ
sec θ = 1/cos θ
tan θ = sin θ/cos θ
cot θ = cos θ/sin θ=1/tan θ

Trigonometric Ratios of Specific Angles

Range of Trigonometric Ratios from 0 to 90 degrees

For $0^{\circ} \leq θ \leq 90^{\circ},$

0≤sinθ≤1
0≤cosθ≤1
0≤tanθ<∞
1≤secθ<∞
0≤cotθ<∞
1≤cosecθ<∞

$t a n θ$ and $s e c θ$ are not defined at $90^{\circ} .$
$c o t θ$ and $c o s e c θ$ are not defined at $0^{\circ} .$

Variation of trigonometric ratios from 0 to 90 degrees

As $θ$ increases from $0^{\circ}$ to $90^{\circ}$

$s i n θ$ increases from $0$ to $1$
$c o s θ$ decreases from $1$ to $0$
$t a n θ$ increases from $0$ to $\infty$
$c o s e c θ$ decreases from $\infty$ to $1$
$s e c θ$ increases from $1$ to $\infty$
$c o t θ$ decreases from $\infty$ to $0$

Standard values of Trigonometric ratios

∠A	0^o	30^o	45^o	60^o	90^o
sin A	0	1/2	1/√2	√3/2	1
cos A	1	√3/2	1/√2	1/2	0
tan A	0	1/√3	1	√3	not defined
cosec A	not defined	2	√2	2/√3	1
sec A	1	2/√3	√2	2	not defined
cot A	not defined	√3	1	1/√3	0

To know more about Trigonometric Ratios of Standard Angles, visit here.

Trigonometric Ratios of Complementary Angles

Complementary Trigonometric ratios

If $θ$ is an acute angle, its complementary angle is 90 $^{\circ} - θ .$ The following relations hold true for trigonometric ratios of complementary angles.

$s i n (90^{\circ} - θ) = c o s θ$
$c o s (90^{\circ} - θ) = s i n θ$
$t a n (90^{\circ} - θ) = c o t θ$
$c o t (90^{\circ} - θ) = t a n θ$
$c o s e c (90^{\circ} - θ) = s e c θ$
$s e c (90^{\circ} - θ) = c o s e c θ$

To know more about Trigonometric Ratios of Complementary Angles, visit here.

Trigonometric Identities

$s i n^{2} θ + c o s^{2} θ = 1$
$1 + c o t^{2} θ = c o e s c^{2} θ$
$1 + t a n^{2} θ = s e c^{2} θ$

To know more about Trigonometric Identities, visit here.

Trigonometry for Class 10 Problems

Example 1:

Find Sin A and Sec A, if 15 cot A = 8.

Solution:

Given that 15 cot A = 8

Therefore, cot A = 8/15.

We know that tan A = 1/ cot A

Hence, tan A = 1/(8/15) = 15/8.

Thus, Side opposite to ∠A/Side Adjacent to ∠A = 15/8

Let BC be the side opposite to ∠A and AB be the side adjacent to ∠A and AC be the hypotenuse of the right triangle ABC respectively.

Hence, BC = 15x and AB = 8x.

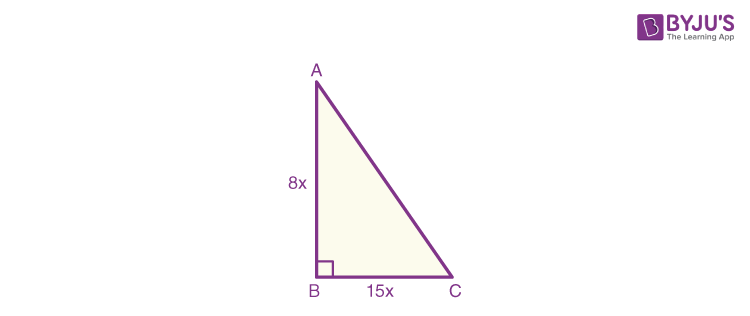
Hence, to find the hypotenuse side, we have to use the Pythagoras theorem.

(i.e) AC² = AB² + BC²

AC² = (8x)²+(15x)²

AC² = 64x²+225x²

AC² = 289x²

AC = 17x.

Therefore, the hypotenuse AC = 17x.

Finding Sin A:

We know Sin A = Side Opposite to ∠A / Hypotenuse

Sin A = 15x/17x

Sin A = 15/17.

Finding Sec A:

To find Sec A, find cos A first.

Thus, cos A = Side adjacent to ∠A / Hypotenuse

Cos A = 8x/17x

We know that sec A = 1/cos A.

So, Sec A = 1/(8x/17x)

Sec A = 17x/8x

Sec A = 17/8.

Therefore, Sin A = 15/17 and sec A = 17/8.

Example 2:

If tan (A+ B) =√3, tan (A-B) = 1/√3, then find A and B. [Given that 0° <A+B ≤ 90°; A>B ]

Solution:

Given that

Tan (A+B) = √3.

We know that tan 60 = √3.

Thus, tan (A+B) = tan 60° = √3.

Hence A+B= 60° …(1)

Similarly, given that,

Tan (A-B) = 1/√3.

We know that tan 30° = 1/√3.

Thus, tan (A-B) = tan 30° = 1/√3.

Hence, A-B = 30° …(2)

Now, adding the equations (1) and (2), we get

A+B+A-B = 60° + 30°

2A = 90°

A = 45°.

Now, substitute A = 45° in equation (1), we get

45° +B = 60°

B = 60°- 45°

B = 15°

Hence, A = 45 and B = 15°.

Stay tuned with BYJU’S – The Learning App and download the app to learn all Maths-related concepts easily by exploring more videos.