Lines and Angles Class 9
CBSE Class 9 Maths Lines and Angles Notes:-Download PDF Here
Lines and Angles for class 9 notes are provided here. The complete notes on lines and angles are given, which covers the various concepts such as parallel lines, transversal, angles, intersecting lines, interior angles are explained with the examples. Go through the below article to learn about lines and angles.
Parallel lines with a transversal
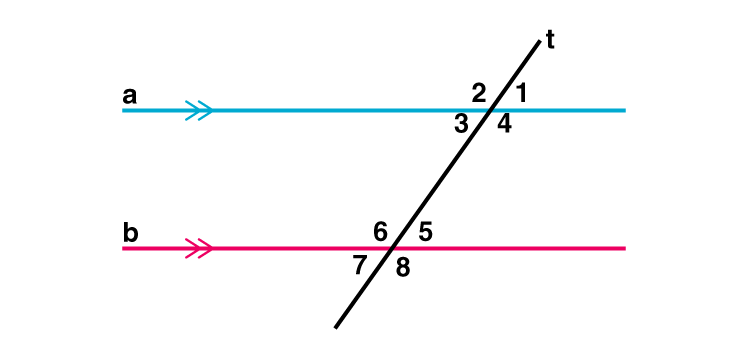
- ∠1=∠5,∠2=∠6,∠4=∠8 and ∠3=∠7(Corresponding angles)
- ∠3=∠5,∠4=∠6 (Alternate interior angles)
- ∠1=∠7,∠2=∠8 (Alternate exterior angles)
Lines parallel to the same line
Lines that are parallel to the same line are also parallel to each other.
For More Information On Parallel Lines and Intersecting Lines, Watch The Below Video:

Introduction to Geometry
Angles and types of angles
When 2 rays originate from the same point at different directions, they form an angle.
– The rays are called arms and the common point is called the vertex
– Types of angles : (i) Acute angle 0∘<a<90∘
(ii) Right angle a=90∘
(iii) Obtuse angle : 90∘<a<180∘
(iv) Straight angle =180∘
(v) Reflex Angle 180∘<a<360∘
(vi) Angles that add up to 90∘ are complementary angles
(vii) Angles that add up to 180∘ are called supplementary angles.
To know more about Angles and Types of Angles, visit here.
Intersecting Lines and Associated Angles
Intersecting and Non-Intersecting lines
- When 2 lines meet at a point they are called intersecting
- When 2 lines never meet at a point, they are called non-intersecting or parallel lines
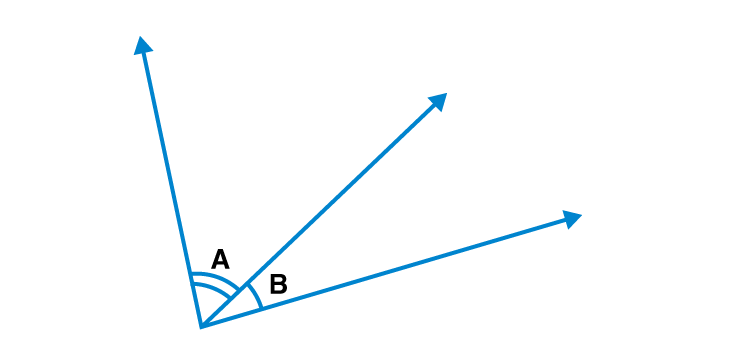
Adjacent angles
2 angles are adjacent if they have the same vertex and one common point.
Linear Pair
When 2 adjacent angles are supplementary, i.e they form a straight line (add up to 180∘), they are called a linear pair.
Vertically opposite angles
When two lines intersect at a point, they form equal angles that are vertically opposite to each other.
To know more about Lines and Angles, visit here.
Basic Properties of a Triangle
Triangle and sum of its internal angles
Sum of all angles of a triangle add up to 180∘
An exterior angle of a triangle = sum of opposite internal angles
– If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles
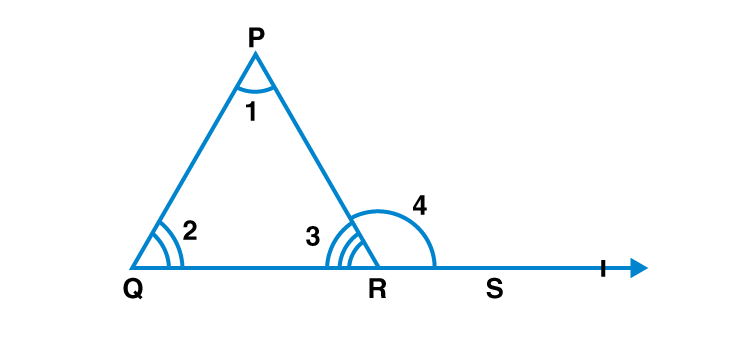
– ∠4=∠1+∠2
For More Information On Properties Of Triangle, Watch The Below Video.

To know more about Properties of a Triangle, visit here.