Conjugate of Complex numbers

Modulus of Complex Number

Let \(z\) = \(x~+~iy\) be a complex number, modulus of a complex number \(z\) is denoted as \(|z|\) which is equal to \(\sqrt{x^{2}+y^{2}}\).

Geometrically, modulus of a complex number \(z\) = \(x ~+ ~iy\) is the distance between the corresponding point of \(z\) which is \((x,y)\) and the origin \((0,0)\) in the argand plane.

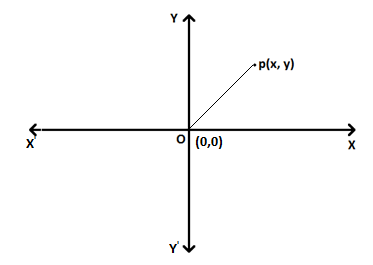
In the above figure, \(OP\) is equal to the distance between the point \((x,y)\) and origin \((0,0)\) in argand plane.

Therefore,

\(|z|\) = \(OP\) = \(\sqrt{x^{2}+y^{2}}\)

Example: Find the value of b if the modulus of the complex number, \(z\) = \(3~+~ib\) is equal to \(5\).

\(|z|\) = \(\sqrt{3^2~+~b^2}\)

\(\sqrt{3^2~+~b^2}\) = \(5\)
\(9~+~b^2\) = \(25\)

\(b^2\) = \(25~-~9\) = \(16\)

\(b\) =\(±4\)

Therefore, \(z\) can be \(3~+~4i\) or \(3~-~4i\).

From the above example, we can conclude that complex numbers \(z_1\) = \(x~+~iy\), \(z_2\) = \( x~-~iy\),

\(z_3\) = \(-x~+~iy\), \(z_4\) = \(-x~-~iy\) will have same modulus which is equal to \(\sqrt{x^2~+~y^2}\). It is because the points corresponding to the above four complex numbers \((x,y)\), \((x,-y)\), \((-x,y)\) and \((-x,-y)\) respectively are at a distance \(\sqrt{x^2~+~y^2}\) away from origin.

Conjugate of a complex number

Conjugate of a complex number \(z\) = \(x~+~iy\)  is  \(x~-~iy \)and which is denoted as \(\overline{z}\).

For example, conjugate of the complex number \(z\) = \(3~-~4i\) is \(3~+~4i\).

• Consider the complex number \(z\) = \(a~+~ib\),
• \(z ~+~ \overline{z}\) = \(a ~+ ~ib~+ ~(a~ – ~ib)\) = \(2a\) which is a complex number having imaginary part as zero.
• \(Re(z ~+~ \overline{z})\) = \(2a\), \(Im(z ~+ ~\overline{z}) \) = \(0\)
• \(z ~-~ \overline{z}\) = \(a~ +~ ib~ – ~(a~ -~ ib)\) = \(2bi\)
• \(Re(z~ -~ \overline{z})\) = \(0\), \(Im(z~ -~ \overline{z})\) = \(2b\)
• Geometrically, reflection of the complex number \(z\) = \(x~+~iy\) in \(X\) axis is the coordinates of \(\overline{z}.\)

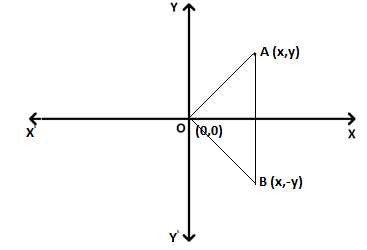
• Modulus of the complex number and its conjugate will be equal.
• Multiplicative inverse of the non-zero complex number \(z\) = \(a~+~ib\) is

\(z^{-1}\) = \(\frac{1}{a~+~ib}\) = \(\frac{a~-~ib}{a^2~+~b^2}\)

Since,\(a~-~ib\) = \(\overline{z}\) and \(a^2~+~b^2\) = \(|z|^2\)

\(z^{-1}\) = \(\frac{z}{|z|^2}\)

\(z\overline{z}\) = \(|z|^2\)

Example: Find the multiplicative inverse of \(z\) = \(6~+~8i\)

\(z^{-1}\) = \(\frac{\overline{z}}{|z|^2}\)

\(\overline{z} = 6 – 8i\) and |z| = \( \sqrt{6^2 + 8^2}\)

= \(\sqrt{100}\) = 10

\(z^{-1}\) = \(\frac{6~-~8i}{100}\) = \(\frac{3-4i}{50}\) = \(\frac{3}{50} – \frac{2}{25} i\)

For any two complex number \(z_1\) and \(z_2\),

• \(|z_1 z_2|\) = \(|z_1 ||z_2 |\)

Let \(z_1\) = \(a~+~ib\) and \(z_2\) = \(c~+~id\),

\(|z_1|\) = \(\sqrt{a^2~+~b^2}\)     —(1)

\(|z_2|\) = \(\sqrt{c^2~+~d^2}\)    —(2)

\(z_1 z_2\) = \((ac~-~bd)~+(bc~+~ad)i\)

\(|z_1 z_2|\) = \( \sqrt{(ac~-~bd)^2~+~(bc~+~ad)}\)

\(|z_1 z_2|^2\) =\((ac~-~bd)^2~+~(bc~+~ad)^2\)

\(=\) \(a^2 c^2~+~b^2 d^2~-~2abcd~+~b^2 c^2~+~a^2 d^2~+~2abcd\)

\(=\) \(a^2 c^2~+~b^2 d^2~+~b^2 c^2~+~a^2 d^2\)

\(=\)\(a^2(c^2~+~d^2)~+~b^2(c^2~+~d^2)\)

\(=\)\((a^2~+~b^2)(c^2~+~d^2 )\)  —(3)

From (1) and (2),

\(|z_1|^2 |z_2 |^2\) = \((a^2~+~b^2)(c^2~+~d^2)\)                 —(4)

Since, (3) = (4);\(|z_1 z_2|\) = \(|z_1||z_2|\)

• Similarly \(z_1\) and \(z_2\), \(|\frac{z_1}{z_2}|\)= \(\frac{|z_1 |}{|z_2 |}\) , provided that \(z_2\) is a non zero complex number.
• \(\overline{z_1z_2}\) = \(\overline{z_1}\overline{z_2}\)
• \(\overline{z_1~ \pm ~z_2}\) = \(\overline{z_1}~\pm~\overline{z_2}\)
• \(\overline{\left(\frac{z_1}{z_2}\right)}\) = \(\frac{\overline{z_1}}{\overline{z_2}}\),provided that \(z_2\) is a non-zero complex number.

Identities of complex numbers

For any two complex numbers \(z_1\) and \(z_2\),

• \((z_1~+~z_2)^2\) = \(z_1^2~+~z_2^2~+~2z_1 z_2\)

We can prove the above identity using the properties of complex numbers.

\((z_1~+~z_2)^2\) = \((z_1~+~z_2)(z_1~+~z_2 )\)

By using distributive law,

\((z_1~+~z_2)(z_1~+~z_2)\) = \(z_1 (z_1~+~z_2)~+~z_2(z_1~+~z_2)\)

= \(z_1^2~+z_1 z_2~+z_2 z_1~+~z_2^2\)—(1)

By using the commutative law, \(z_1 z_2\) = \(z_2 z_1\)

Then (1) will become as,

• \((z_1~+~z_2)^2\) = \(z_1^2~+~z_2^2~+~2z_1 z_2\)
• \((z_1~-~z_2)^2\) = \(z_1^2~+~z_2^2~-~2z_1 z_2\)
• \((z_1~+~z_2)^3\) = \(z_1^3~+~3z_1^2 z_2~+~3z_1 z_2^2~+~z_1^3\)
• \((z_1~-~z_2)^3\) = \(z_1^3~-~3z_1^2 z_2~+~3z_1 z_2^2~-~z_1^3\)
• \(z_1^2~-~z_2^2\) = \((z_1~+~z_2)(z_1~-~z_2)\)<

To know more about the complex numbers and its properties, download BYJU’S – The learning app.

‘